イントロダクション
二次錐計画法(SOCP)は、凸二次制約付き二次計画問題(QCQP)を含む、様々な種類の凸問題を効率的かつ堅牢に解決する方法です。そのため、金融など幅広い分野で高度に活用されています。nAGライブラリのMark 29.3では、SOCPソルバー(nag_opt_handle_solve_socp_ipm)のパフォーマンス更新が導入されました。これは特にポートフォリオ最適化において効果的であることが示されています。
nAGライブラリにおけるSOCPの紹介
二次錐計画法は、ポートフォリオ構築などの応用で発生するQCQP問題を解くための主要な方法の一つです。標準形の凸QCQP問題は以下のように表されます:
\[ \begin{align} & \text{最小化} && \frac{1}{2}x^TQ_0x + r_0^Tx \\ & \text{制約条件} && \frac{1}{2}x^TQ_ix + r_i^Tx + s_i \leq 0, \quad i = 1, \ldots, m \\ & && Ax = b, \end{align} \]
ここで、(Q_{o}, , Q_{m} ) は正半定値 (n n) 行列です。
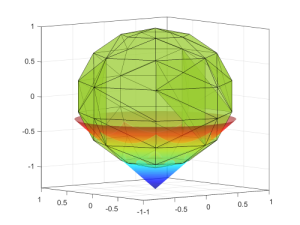
図1:3変数のSOCP問題の実行可能領域
SOCP問題(例えば、変換されたQCQP問題)の実行可能領域は図1で見ることができます。ここでの実行可能領域は、緑色の多面体と円錐の交差部分です。曲線は追加された二次情報を表しており、これによってSOCPは線形計画法よりも複雑になりますが、同時により強力になります。
nAGのSOCPソルバーの実装に関しては、経路追従型同次自己双対アルゴリズムが使用されています。これは堅牢かつ効率的で、モデルの実行不可能性と無限解の検出が可能です。また、nAGは問題のスパース性パターンを徹底的に活用しており、特に大規模でスパースな問題に対してソルバーを効率的にしています。実装の詳細については、nAG SOCPソルバー nag_opt_handle_solve_socp_ipm のnAGライブラリルーチンドキュメントをご覧ください[1]。
ポートフォリオ最適化におけるSOCPの使用
二次錐(SOC)がモデルに自然に現れることは稀ですが、モデルの再構築を通じて、多くのポートフォリオ最適化問題と制約条件をSOCPで扱うことができます。以下でいくつかを説明します。より多くの例については[2]を参照してください。
ノルムを用いた最適化
レバレッジ制約:
\[ \|x\|_1 = \sum_{i=1}^n |x_i| \leq L \iff \sum_{i=1}^n s_i \leq L, \quad (s_i, x_i) \in K_q^2, \quad i = 1, \ldots, n, \]
上記のノルム制約は、ベクトル (x ^n) に対する一般的な (p)-ノルム制約の特殊ケースとみなすことができます。一般的な (p)-ノルム制約は以下のように定義されます:
\[ \|x\|_p := \left( \sum_{i=1}^n |x_i|^p \right)^{1/p} \leq t, \]
ここで、(p = l / m ) は正の有理数で、( l m ) です。不等式制約(1)は有理べき乗を含む不等式と等価であるため、SOC表現を持ちます。
二次制約
トラッキングエラー制約:
\[ \frac{1}{2}x^TPx + q^Tx + r \leq 0, \]
ここで (P S^n) は正半定値行列であり、これはポートフォリオ最適化でよく見られます。Mark 27.1のnAGライブラリで導入されたルーチン handle_set_qconstr (e04rs) と handle_set_qconstr_fac (e04rt) を使用することで、ユーザーは二次目的関数や制約を容易に定義し、他の制約とシームレスに統合することができます。その後、内部で以下のような処理が行われます。行列 (P) が因数分解 (P = F^TF) を持つと仮定すると、(2)は以下のSOC表現と等価になります:
\[ t + q^Tx + r = 0, \quad (t, 1, Fx) \in K_r^{n+2}, \]
これは ((1 / 2)x^TPx t ) が ( | Fx |^2_{2} 2t) と等価であるためです。したがって、補助変数 (y = Fx) を追加することで、二次制約を標準的な錐制約に変換します。
詳細については、QCQPに関するミニ記事と二次関数を含むポートフォリオ最適化のPythonの例をご覧ください。
その他の二次錐表現可能な関数
上記で重要なSOC表現可能な関数について言及しましたが、ポートフォリオ最適化からの多くの問題や制約がSOC表現可能です。以下にいくつか挙げます。
- 市場インパクト最小化:ポートフォリオリターンの分散を制約することで、期待取引コストを最小化します。
- リスクパリティ:各資産がポートフォリオ全体のリスクに均等に寄与するように資本を配分します。
- カーディナリティ制約:ポートフォリオ内のゼロでない位置の数を制限します。
- 最小取引単位制約:取引される各資産の数量が指定された単位の整数倍であることを保証します。
これらの制約の詳細な説明と実装はこの記事の範囲を超えていますが、nAGライブラリのドキュメントとサンプルコードで利用可能です。
結論
SOCPは凸最適化の分野における強力なツールであり、特にポートフォリオ最適化のような金融アプリケーションで有用です。nAGライブラリの更新により、ユーザーは大規模で複雑な問題を扱える効率的で堅牢なソルバーにアクセスできるようになりました。SOCPを活用することで、ユーザーは様々な制約と目的を組み込みながら、最適化された解を得ることができます。
