nAG最適化コーナー: 問題に適したソルバーを選ぶ（密 - スパース）

この記事はnAG最適化コーナー シリーズの一部です。 このコーナーではこれまでに、問題の種類に合わせて適切なソルバーを選択することの重要性を示し、そうしないと計算資源を大幅に浪費してしまう可能性があることを示してきました。

問題に最適なソルバーを見つける事は必ずしも簡単ではありませんが、数理最適化ソルバー選択ガイドが役に立ちます。ガイドに含まれる決定木は一連の質問で構成されていますが、その最初の質問は

「問題はスパース／大規模ですか？」

ここから本記事は、この質問の重要性を示すために2つのタイプの最適化問題を示し、この質問に対してどのように答えるかについてのガイダンスを提供します。

スパース性（sparsity）とは？

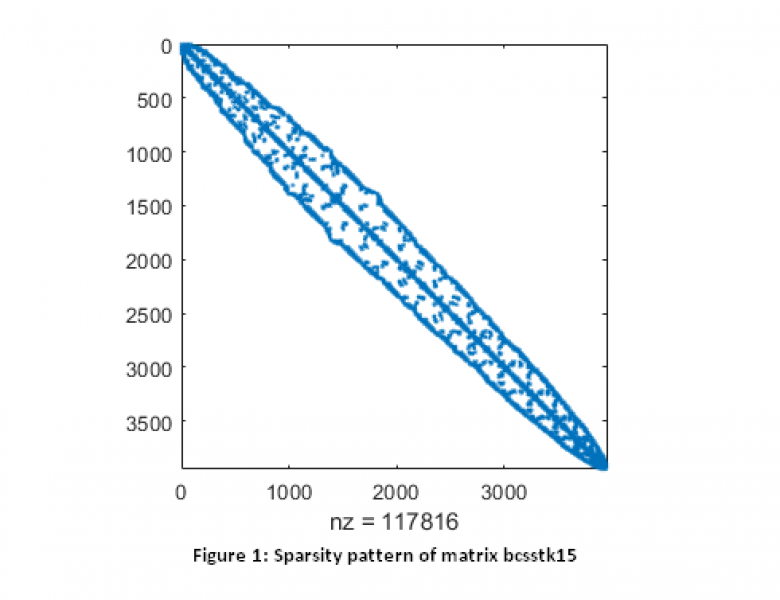
行列のエントリーがほとんどゼロの場合、その行列をスパース（疎）と呼びます。スパース問題のデータ表現は、通常、線形制約行列または非線形制約のヤコビ行列を定義するスパース行列の形式になります。大規模な問題は、通常、かなり多くの変数と制約を持っていますが、すべての変数に関係する制約はごく少数であり、ほとんどの制約は変数の小さなサブセットにのみ依存します。つまりこれは、問題がスパースであるという事です。図1は、n=3948次元の疎行列の疎パターンを示しており、密度=nnz/n2=0.756%でこれが1%以下であることから、かなりスパースであることがわかります。問題にスパースな構造が存在する場合、それを捉えて適切なソルバーに渡すことが重要です。専門のソルバーは、行列のスパースな構造を利用して、ゼロに対する計算とメモリの浪費を防ぎます。

コレスキー分解におけるスパース性の影響

問題のスパース性を利用することの重要性を強調するために、凸最適化における内点法（IPM）などの数値アルゴリズムで広く利用されているコレスキー分解の例を見てみましょう。世界中の大規模な最適化ソルバーは、数値的な安定性と効率性を両立させるために、行列分解の際にスパース性パターンを非常に注意深く利用しています。

実対称の正定値行列Mのコレスキー分解とは、M=LL^T（Lは下三角行列）となるような因子Lを見つけることです。ここでは、Matrix Market [1]から、構造工学や構造力学などの分野で使用される9つの正定値行列を選択しました。表1に示すように、すべての行列は、密度が1.5%未満とかなり疎です。

前述したように、非ゼロのエントリのみを格納することでメモリ要件を削減し、スパース・パターンを利用することで計算コストを大幅に削減することができます。この点を説明するために、選択したデータセットでスパースのコレスキールーチンと密のコレスキールーチンをテストし、その結果を図2に示しました。すべてのテストケースにおいて、スパースのコレスキールーチンは密のコレスキールーチンよりも速いことがわかります。その理由は、密のアルゴリズムが行列の次元に関連しているのに対し、疎のアルゴリズムは主に非ゼロの数に関連していることから、想像に難くありません。問題8と9では、問題サイズが大きく変化したため、密のアルゴリズムの性能が大きく低下していますが、スパースのアルゴリズムでは、すべてのテストケースで密度がかなり低く抑えられているため、一様に良好な性能が得られています。

図2：スパースと密のコレスキーの計算時間の比較

スパース性がアルゴリズムの性能にどのように影響するかをさらに説明するために，サイズ1000，3000，5000の対称正定値行列をランダムに生成しました。行列によってはそのサイズにより，密度は 10% から 100% の範囲で変化します。そして、スパースのコレスキーと密のコレスキーの両ルーチンを呼び出して行列を分解し、その計算時間を比較した結果を図3に示します。意外なことに、同じサイズの行列の場合、密度が高くなっても密コレスキーの時間はあまり変わりません。しかし、スパースコレスキーは、行列の密度が高くなるにつれて、より多くの時間がかかり、ある時点で、密のアルゴリズムよりも多くの計算時間を必要とします。比較的密度の高い行列（20%以上など）では、トレードオフが成り立たなくなり、密の方が良い選択となります。

図3：サイズ1000、3000、5000の行列に対する
分解法の比較：様々な密度

線形計画法(LP)の例

一般的なLP問題は、以下のような形をしています。

（1） $$\begin{array}{cc}\underset{x\in {\Re }^n}{\text{minimize}}\hfill & c^{T}x\hfill \\ & \\ \text{subject to}\hfill & Ax=b,\hfill \\ & \\ \hfill & x\ge 0.\hfill \end{array}$$

ここでは、nAGライブラリの2つのアクティブセット法ルーチンlp_solve（e04mf）（密ソルバー）とqpconvex2_sparse_solve（e04nq）（スパースソルバー）を用いて上記モデルを解きました。その結果を表2に示します。どちらのテストケースも密度は1.0%以下であり、密ソルバーが著しく遅かったのに対し、e04nqはどちらのケースでも1秒以下の処理時間でした。つまりスパースな問題を密ソルバーに与えるとパフォーマンスが劇的に悪くなっている事がわかります。

専用ソルバー

最近nAGライブラリーユーザから、以下の $l_1$ 線形フィッティング問題についてテクニカルサポートのお問い合わせいただきました。

（2） $$\begin{array}{cc}\underset{x\in {\Re }^n}{\text{minimize}}\hfill & \parallel Ax-b{\parallel }_1\hfill \end{array}$$

ここで、行列Aは背の高いスリムなもので、例えば1000×21次元の密行列です。問題データAとbにゼロがないため、一見すると密な問題のように見えるかもしれません。 $l_1$ ノルム最小化は線形計画法に変換できるので、ユーザーはこの変換を行い、アクティブセット法のlp_solve（e04mf）（dense solver）を用いて問題を解きましたが、期待したほど高速ではなかったことから、我々にお問い合わせをいただきました。

このような誤解や混乱は珍しいことではなく、注意が必要です。問題がスパースなのか密なのかを判断するためには、元のデータではなく、ソルバーが解く問題モデルのデータを考える必要があります。例えば、問題（2）は以下のLP問題に再定式化できます。

（3） $$\begin{array}{cc}\underset{x\in {\Re }^n,y\in {\Re }^m}{\text{minimize}}\hfill & \sum _i{y}_i\hfill \\ & \\ \text{subject to}\hfill & -y\le Ax-b\le y,\hfill \\ & \\ \hfill & y\ge 0.\hfill \end{array}$$

不等式の制約条件をよく見てみると以下のようになっています。 $$-y\le Ax-b\le y\iff \left(\begin{array}{cc}\hfill A\hfill & \hfill -I\hfill \\ \hfill -A\hfill & \hfill -I\hfill \end{array}\right)\left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right)\le \left(\begin{array}{c}\hfill b\hfill \\ \hfill -b\hfill \end{array}\right),$$

ここで、Iはm次元の単位行列であり、変数の数がm個増加し、モデルに多くのゼロエントリが導入されていることがわかります。 したがって、この特殊なモデルには、スパースなLPソルバーが適切です。

nAGライブラリのアクティブセット法ソルバーlp_solve（e04mf）とスパース内点法ソルバーhandle_solve_lp_ipm（e04mt）を用いて、次元1000×21の行列Aでテストを行いました。

表3に見られるように、スパースなLPソルバーは密のソルバーと比較して再び素晴らしい性能を示しています。

明らかに、スパースソルバーが計算時間を向上させている理由です。しかし、問題（2）に対する専用ソルバーglin_l1sol（e02ga）は、既知の問題構造を徹底的に利用しているため、スパースLPソルバーよりもさらに良い結果となりました。この専用ソルバーは、最初の試みに比べて7100倍のスピードアップを実現しました。したがって、特定の問題については、まず専用ソルバーを試すことを常に推奨します。専用ソルバーはこのブログの範囲からは少し外れますが、専用ソルバーで提供されるnAGの全内容についてはnAGライブラリのドキュメントをご覧ください。

覚えておくと役立つ事

スパース性は素晴らしい機能ですが、慎重に検討する必要があります。 問題に根本的なスパース構造がある場合、スパースソルバーを選択してください。そうでない場合は、パフォーマンスを著しく損なうことになります。 再定式化が必要な場合は、元のデータではなく、ソルバーが見ているデータ構造を分析することが重要です。 まずは、専用のソルバーを探すことをお忘れなく。

---

本記事は以下の原文（英語）を翻訳したものです。
https://www.nag.com/blog/optcorner-right-tool-job-dense-v-sparse

さらに詳しくお知りになりたい場合はお気軽に お問い合わせ 下さい。