このページは、nAGライブラリのJupyterノートブックExampleの日本語翻訳版です。オリジナルのノートブックはインタラクティブに操作することができます。
CVXPYを介したnAG二次錐計画法による分類
このノートブックの正しいレンダリング
このノートブックは、方程式と参照のためにlatex_envs
Jupyter拡張機能を使用しています。LaTeXがJupyterのローカルインストールで適切にレンダリングされない場合、この拡張機能をインストールしていない可能性があります。詳細は
https://jupyter-contrib-nbextensions.readthedocs.io/en/latest/nbextensions/latex_envs/README.html
を参照してください。
nAGライブラリのインストールとこのノートブックの実行
このノートブックを実行するにはnAGライブラリが必要です。ライブラリをダウンロード、インストール、ライセンスを取得するには、index.htmファイルの指示をお読みください。
ノートブックの実行方法はこちらで見つけることができます。
はじめに
このノートブックでは、nAGの二次錐計画法(SOCP)ソルバーを使用して、平面上の2つの点集合を頑健に分離する4次多項式 \[\begin{equation}\label{poly} p(x,y) = \sum_{i,j} a_{ij} x^i y^j ~\mbox{with}~ i+j\leq4 \end{equation}\] を見つける方法を示します。この問題の最適化モデルは次のように表現できます: \[\begin{equation}\label{prob} \begin{array}{ll} \underset{a\in\Re^{15}}{\mbox{minimize}} & \|a\|\\[0.6ex] \mbox{subject to} & p(x,y)\leq -1, \mbox{for x, y in set 1},\\[0.6ex] & p(x,y)\geq 1, \mbox{for x, y in set 2}. \end{array} \end{equation}\]
# 必要なパッケージをインポート
import numpy as np
import cvxpy as cvx
import matplotlib.pyplot as pltデータの準備
このセクションでは、モデルのトレーニングデータとして使用する2セットのランダムな点を生成します。
# 乱数シードを固定する
np.random.seed(3)
# 2つの主要な点の集合を生成する
# 各集合の点の数
n = 80
set_1_base = np.random.uniform(-1.0, 1.0, (n,2))
set_2_base = np.random.uniform(-1.0, 1.0, (n,2))
# セット1がセット2に囲まれるように主要な点をスケーリングする
for i in range(n):
set_1_base[i,0:] = 0.9 * set_1_base[i,0:] * np.random.rand() / \
np.linalg.norm(set_1_base[i,0:])
set_2_base[i,0:] = set_2_base[i,0:] * (1.1 + np.random.rand() / \
np.linalg.norm(set_2_base[i,0:]))
# データをさらに処理して、点の集合の異常な形状を作成する
maxnorm_set_1 = max(np.linalg.norm(set_1_base,axis=1))
set_2_pick = set_2_base[np.linalg.norm(set_2_base,axis=1)>maxnorm_set_1,0:]
set_1_pick = np.concatenate((set_1_base,
set_2_base[np.linalg.norm(set_2_base,axis=1)<=
maxnorm_set_1,0:]))
# セット1の形状は主に丸いです。私は左からセット1を押して異常にします。
# パンチ力を自由に変更して、結果のグラフを確認してください
punch_power = 1.0
set_1 = set_1_pick[np.linalg.norm(set_1_pick-[-1.0,-0.5],axis=1)>punch_power,0:]
set_2 = np.concatenate((set_2_pick,
set_1_pick[np.linalg.norm(set_1_pick-[-1.0,-0.5],axis=1)<=
punch_power,0:]))これでトレーニングデータの準備が整いました。可視化してみましょう。
data = (set_1, set_2)
colors = ("red", "blue")
groups = ("set1", "set2")
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1, alpha=1.0)
for data, color, group in zip(data, colors, groups):
x = data[0:,0]
y = data[0:,1]
ax.scatter(x, y, alpha=0.8, c=color, edgecolors='none', s=10, label=group)
plt.xlim(-2.0, 2.0)
plt.ylim(-2.0, 2.0)
plt.title('Training Data')
plt.legend(loc=2)
plt.show()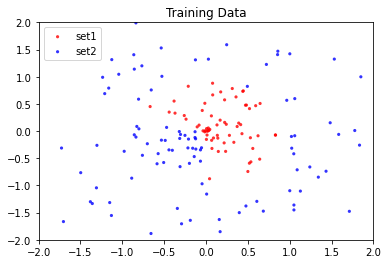
4次多項式の係数の数は\(15\)であり、これが変数の数となります。
# 変数の数
nvar = 15制約式(prob)の両方の制約は変数\(a\)に関して線形です。これらの制約の線形係数を設定するには、set_1とset_2を使用してください。
A_1 = np.zeros((set_1.shape[0], nvar))
A_2 = np.zeros((set_2.shape[0], nvar))
for i in range(set_1.shape[0]):
counter = 0
for j in range(5):
for k in range(5-j):
A_1[i,counter] = set_1[i,0]**j * set_1[i,1]**k
counter = counter + 1
for i in range(set_2.shape[0]):
counter = 0
for j in range(5):
for k in range(5-j):
A_2[i,counter] = set_2[i,0]**j * set_2[i,1]**k
counter = counter + 1CVXPYを使用して問題をモデル化し解く
# 意思決定変数を定義する
x = cvx.Variable(nvar)
# 目的関数を定義する
objective = cvx.Minimize(cvx.norm(x))
# 制約条件を定義する
constraint = [A_1@x <= -1.0, A_2@x >= 1.0]
# 問題全体を定義する
problem = cvx.Problem(objective, constraint)
# 解け、Bing!
problem.solve(solver='nAG', verbose=True)
# 結果を保存
coef = x.value ------------------------------------------------
E04PT, Interior point method for SOCP problems
------------------------------------------------
Begin of Options
Print File = -1 * U
Print Level = 2 * d
Print Options = Yes * d
Print Solution = No * d
Monitoring File = 6 * U
Monitoring Level = 2 * U
Socp Monitor Frequency = 0 * d
Infinite Bound Size = 1.00000E+20 * d
Task = Minimize * d
Stats Time = No * d
Time Limit = 1.00000E+06 * d
Socp Iteration Limit = 100 * d
Socp Max Iterative Refinement = 9 * d
Socp Presolve = Yes * d
Socp Scaling = None * d
Socp Stop Tolerance = 1.05367E-08 * d
Socp Stop Tolerance 2 = 1.05367E-08 * d
Socp System Formulation = Auto * d
End of Options
Problem Statistics
No of variables 32
bounds not defined
No of lin. constraints 176
nonzeroes 2432
No of quad.constraints 0
No of cones 1
biggest cone size 16
Objective function Linear
Presolved Problem Measures
No of variables 191
No of lin. constraints 175
nonzeroes 2590
No of cones 1
------------------------------------------------------------------------
it| pobj | dobj | p.inf | d.inf | d.gap | tau | I
------------------------------------------------------------------------
0 1.00000E+00 0.00000E+00 2.70E-02 5.35E-03 2.00E+00 1.0E+00
1 5.13493E+01 8.32818E+01 1.29E-02 2.55E-03 9.55E-01 5.0E-02
2 2.80351E+01 5.34418E+01 9.73E-03 1.93E-03 7.22E-01 3.6E-01
3 1.11360E+02 2.17980E+02 4.46E-03 8.86E-04 3.31E-01 1.2E-01
4 2.07571E+02 4.06965E+02 2.08E-03 4.13E-04 1.55E-01 5.9E-02
5 3.02366E+02 5.91847E+02 1.38E-03 2.74E-04 1.03E-01 3.5E-02
6 2.42309E+02 4.51372E+02 2.93E-04 5.82E-05 2.18E-02 2.0E-02
7 1.29884E+02 1.56324E+02 8.30E-05 1.65E-05 6.16E-03 2.2E-02
8 7.71822E+01 8.68099E+01 3.34E-05 6.63E-06 2.48E-03 3.4E-02
9 6.67725E+01 7.13985E+01 1.75E-05 3.48E-06 1.30E-03 3.6E-02
10 6.49722E+01 6.63180E+01 7.68E-06 1.52E-06 5.70E-04 3.2E-02
11 6.27050E+01 6.28895E+01 2.58E-06 5.11E-07 1.91E-04 3.2E-02
12 6.17692E+01 6.18968E+01 1.62E-06 3.21E-07 1.20E-04 2.9E-02
13 6.14587E+01 6.14705E+01 4.56E-07 9.04E-08 3.38E-05 2.9E-02
14 6.11965E+01 6.11981E+01 5.12E-08 1.02E-08 3.80E-06 2.8E-02
15 6.11753E+01 6.11754E+01 2.23E-09 4.43E-10 1.66E-07 2.8E-02
16 6.11747E+01 6.11747E+01 8.75E-11 1.72E-11 6.42E-09 2.8E-02
------------------------------------------------------------------------------
Status: converged, an optimal solution found
------------------------------------------------------------------------------
Final primal objective value 6.117468E+01
Final dual objective value 6.117469E+01
Absolute primal infeasibility 6.493819E-09
Relative primal infeasibility 8.753236E-11
Absolute dual infeasibility 3.212062E-09
Relative dual infeasibility 1.718111E-11
Absolute complementarity gap 6.424124E-09
Relative complementarity gap 6.424124E-09
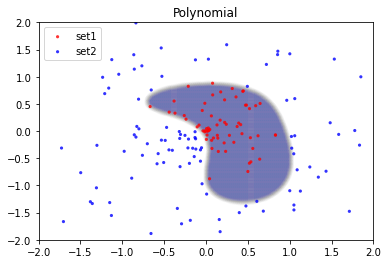
Iterations 16分類器を可視化する
# メッシュを生成する
x = np.arange(-5.0,5.0,0.008)
y = np.arange(-5.0,5.0,0.008)
xx, yy = np.meshgrid(x,y)
# メッシュ上の多項式の値
polyval = np.zeros(xx.shape)
counter = 0
for i in range(5):
for j in range(5-i):
polyval = polyval + coef[counter]*np.power(xx,i)*np.power(yy,j)
counter = counter + 1
# 訓練された多項式をプロットする
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1, alpha=1.0)
ax.scatter(xx[polyval<=-1], yy[polyval<=-1], alpha=0.002)
data = (set_1, set_2)
colors = ("red", "blue")
groups = ("set1", "set2")
for data, color, group in zip(data, colors, groups):
x = data[0:,0]
y = data[0:,1]
ax.scatter(x, y, alpha=0.8, c=color, edgecolors='none', s=10, label=group)
plt.xlim(-2.0, 2.0)
plt.ylim(-2.0, 2.0)
plt.title('Polynomial')
plt.legend(loc=2)
plt.show()