このページは、nAGライブラリのJupyterノートブックExampleの日本語翻訳版です。オリジナルのノートブックはインタラクティブに操作することができます。
粒子群最適化の例
このノートブックは、nAG Library for Pythonを使用してnAG粒子群最適化(PSO)ソルバーで大域的最適化問題を解く方法を示す短い例です。
PSOは、遺伝的アルゴリズム、シミュレーテッドアニーリング、アントコロニー最適化などと同様の振る舞いをするヒューリスティックアルゴリズムです。探索空間に粒子の集合(群れ)が生成され、各反復で個々の粒子が見つけた最良の候補(認知メモリ)、すべての粒子が見つけた最良の候補(グローバルメモリ)、および慣性に基づくヒューリスティックな速度に従って前進します。慣性は、粒子の現在の速度からの減少重み付け寄与によって提供されます。この組み合わせにより、問題のドメインの大域的な探索が可能になります。
群れが潜在的な最適解の周りで収縮および拡大する速度はユーザーが制御可能で、専門知識が利用可能な場合に使用できます。さらに、このアルゴリズムは、さまざまな局所最適化手法と組み合わせることができます。これらは、ヒューリスティックアルゴリズムの反復中(内部フェーズ)に呼び出され、局所的に最適な点の発見を加速することができます。また、ヒューリスティックな反復の後(外部フェーズ)に呼び出され、最終解を改善しようとすることもできます。各フェーズで局所最適化手法に対して異なるオプションを設定できます。
最適化アルゴリズムのテストによく使用されるAckley関数を最小化します:
\[f(x_0 \cdots x_n) = -20 exp(-0.2 \sqrt{\frac{1}{n} \sum_{i=1}^n x_i^2}) - exp(\frac{1}{n} \sum_{i=1}^n cos(2\pi x_i)) + 20 + e)\]
PSOがこの特定の関数を解くための最良の方法であると提案しているわけではなく、単に例として使用しています。
まず、matplotlibを使用して実行可能領域上の関数をプロットすることから始めることができます:
# Jupyter の表示バックエンドを選択:
%matplotlib inline
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
def ackley(x, y):
return (
-20.0*np.exp(-0.2*np.sqrt((x**2+y**2)/2)) -
np.exp(0.5*(np.cos(2.0*np.pi*x) + np.cos(2.0*np.pi*y))) +
20 + np.e
)
# X,Y グリッドを生成する
X, Y = np.meshgrid(np.arange(-5.,5.,0.01), np.arange(-5.,5.,0.01))
# その格子上でアックリー関数を計算する
Z = ackley(X, Y)
fig = plt.figure(figsize=(20,10))
ax = Axes3D(fig, auto_add_to_figure=False)
ax.set_xlim3d(-5, 5)
ax.set_ylim3d(-5, 5)
ax.set_zlim3d(0, 15)
ax.plot_surface(X, Y, Z, cmap=cm.jet, linestyles="solid")
ax.plot_wireframe(X, Y, Z, color='black', lw=0.5, rstride=10, cstride=20)
lev = [0.1, 1, 2, 3, 4, 5, 6, 7, 8, 10]
ax.contour(X, Y, Z, levels=lev, colors='black', linestyles="solid", offset=-1)
fig.add_axes(ax)
plt.show()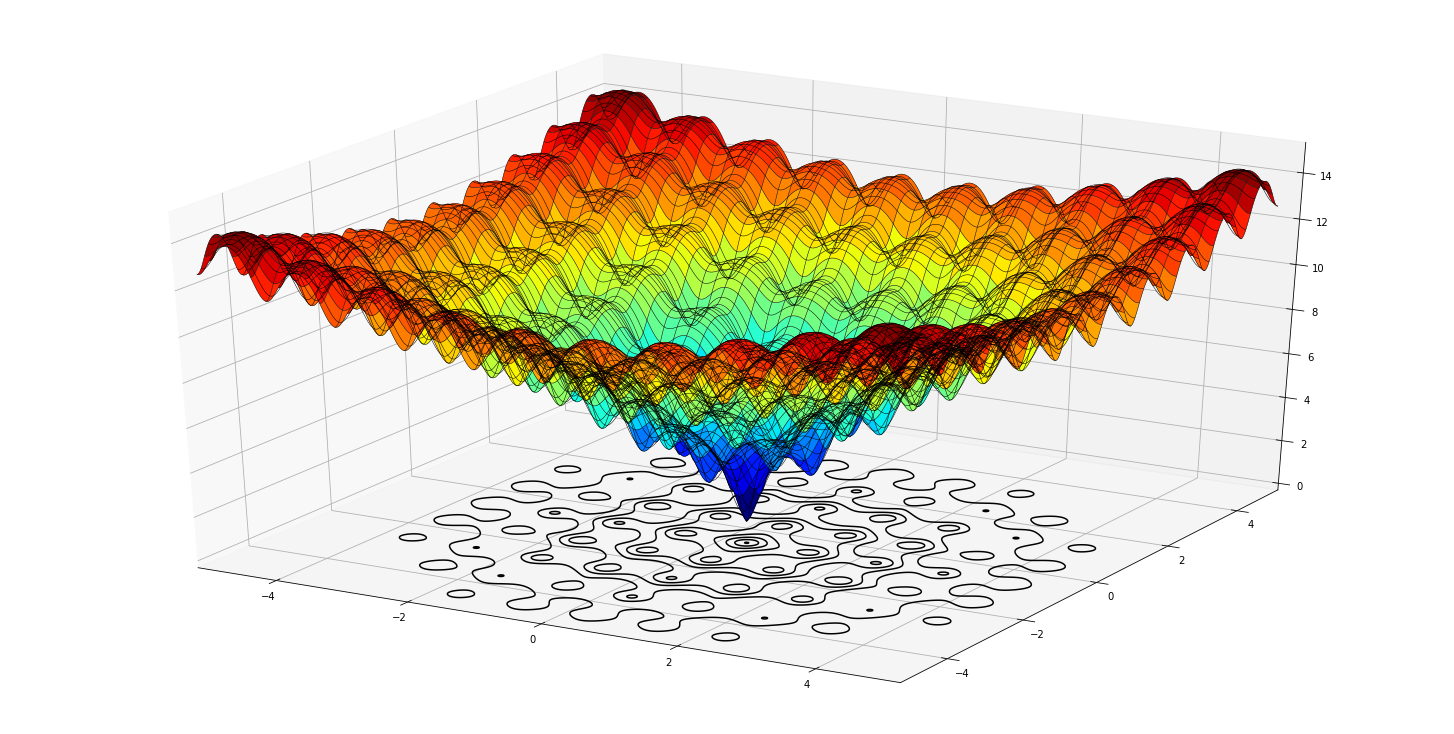
この関数は、多くの局所的最小値を持つように設計されていますが、x=0.0とy=0.0にのみグローバルな最小値があります。 多くの局所的最小値は、一部のソルバーに問題を引き起こす可能性があります。
デフォルト設定でPSOを使用して解く
目的関数を正しい形式で記述する
最初に行う必要があるのは、PSOソルバーに適した方法で目的関数を定義することです。アックリー関数の元の定義は以下の通りです:
def ackley(x,y):
return -20.0*np.exp(-0.2*np.sqrt((x**2+y**2)/2)) - np.exp(0.5*(np.cos(2.0*np.pi*x)+np.cos(2.0*np.pi*y))) + 20 + np.eこれはソルバーが少なくとも4つの入力と正確に2つの出力を持つ目的関数を期待しているため、機能しません:
def objfun(mode, x, objf, vecout, nstate):
#ここで目的関数を計算し、関数値をobjfとして返す
return objf, vecoutこれらの引数の意味については後で詳しく説明します(または完全なドキュメントに飛んで詳細を確認できます)が、今のところ、入力ベクトルinと入力/出力ベクトルobjfおよびvecoutだけを気にする必要があります。
xには、目的関数を評価したいN次元点の座標のベクトルが含まれていますobjfには点xにおける目的関数の値が含まれていますvecoutは、より高度な使用法では、vecoutを使用して目的関数の勾配を格納できます。ここでは使用されず、サイズNである限り何でも構いません。ゼロのベクトルで問題ありません
したがって、上記のackley(x,y)関数を使用して目的関数を定義できます:
# PSO ソルバーが求める形式の目的関数
# 入力引数をすべて使用する必要はありません。関数定義に含まれていればよいのです。
def objfun(_mode, x, objf, vecout, _nstate):
# 以前に定義されたアックリー関数を使用して目的関数を評価する
objf = ackley(x[0], x[1])
return objf, vecoutPSOソルバーをセットアップし、デフォルト設定で実行する
ここで、変数の境界を設定し、ソルバーを初期化して実行します
# グローバル最適化の章をインポートする
from naginterfaces.library import glopt
# 変数の境界
bl = [-5., -5.] # Lower bounds for each dimension
bu = [5., 5.] # Upper bounds for each dimension
# ソルバーをデフォルト設定で初期化する
options = {}
glopt.optset('Initialize = bnd_pso', options)
# ソルバーを実行する
sol_x, fun_x, itt, inform = glopt.bnd_pso(bl, bu, objfun, options)
# 解答を表示する
print('The solver converged with inform = {0} Refer to the documentation to see what this means'.format(inform))
print('The minimum was found at the point {0},{1}'.format(sol_x[0], sol_x[1]))
print('The value of the objective function at this point is {0}'.format(fun_x))
print('The number of function evaluations was {0}'.format(itt[4]))The solver converged with inform = 2 Refer to the documentation to see what this means
The minimum was found at the point 0.0,0.0
The value of the objective function at this point is 4.440892098500626e-16
The number of function evaluations was 1296
<ipython-input-3-5022195bb130>:13: NagAlgorithmicWarning: (nAG Python function naginterfaces.base.glopt.bnd_pso, code 1:1,10101)
** A finalization criterion was reached that cannot guarantee success.
** On exit, inform = 2.
sol_x, fun_x, itt, inform = glopt.bnd_pso(bl, bu, objfun, options)ソルバーはx = 0.0、y = 0.0で大域的最小値を見つけました
再現可能な結果
粒子群最適化は確率的アルゴリズムであり、その動作の一部として乱数を使用します。そのため、実行ごとに結果が異なる可能性があります。例えば、最適解が変わる可能性があり、関数評価の回数も変わる可能性があります。これがデフォルトの動作です。
上のセルを繰り返し実行すると、関数評価の回数が変わることがわかります。これは比較的簡単な問題なので、見つかった大域的最小値はおそらく変わらないでしょう。
必要に応じて、再現可能モードをオンにしてランダムシードを設定することで、結果を再現可能にすることができます
# ソルバーを初期化する
options = {}
glopt.optset('Initialize = bnd_pso', options)
glopt.optset('Repeatability = ON', options)
glopt.optset('Seed = 1', options) # Could have used any integer
# ソルバーを実行する
sol_x, fun_x, itt, inform = glopt.bnd_pso(bl, bu, objfun, options)
# 解答を表示する
print('The solver converged with inform = {0} Refer to the documentation to see what this means'.format(inform))
print('The minimum was found at the point {0},{1}'.format(sol_x[0], sol_x[1]))
print('The value of the objective function at this point is {0}'.format(fun_x))
print('The number of function evaluations was {0}'.format(itt[4]))The solver converged with inform = 2 Refer to the documentation to see what this means
The minimum was found at the point 0.0,0.0
The value of the objective function at this point is 4.440892098500626e-16
The number of function evaluations was 1385
<ipython-input-4-3435fedb1173>:8: NagAlgorithmicWarning: (nAG Python function naginterfaces.base.glopt.bnd_pso, code 1:1,10101)
** A finalization criterion was reached that cannot guarantee success.
** On exit, inform = 2.
sol_x, fun_x, itt, inform = glopt.bnd_pso(bl, bu, objfun, options)上記のセルで再現性モードをオンにし、乱数シードを1に設定しました。すべての実行で同じ解と正確に1385回の関数評価が得られます
出力警告のフィルタリング
PSOソルバーはかなり冗長で、グローバル最小値が見つかったかどうか完全には確信できないという警告を発します。解の状態は
inform
変数にも含まれているため、警告をオフにしてノートブックをより整理された状態にすることもできます。
import warnings
from naginterfaces.base import utils
warnings.simplefilter("ignore", utils.NagAlgorithmicWarning)ソルバーを再度実行し、警告が出力されないことを確認してください
# ソルバーを初期化する
options = {}
glopt.optset('Initialize = bnd_pso', options)
glopt.optset('Repeatability = ON', options)
glopt.optset('Seed = 1', options) # Could have used any integer
# ソルバーを実行し、警告が発生しないことを確認します
sol_x, fun_x, itt, inform = glopt.bnd_pso(bl, bu, objfun, options)
# 解答を表示する
print('The solver converged with inform = {0} Refer to the documentation to see what this means'.format(inform))
print('The minimum was found at the point {0},{1}'.format(sol_x[0], sol_x[1]))
print('The value of the objective function at this point is {0}'.format(fun_x))
print('The number of function evaluations was {0}'.format(itt[4]))The solver converged with inform = 2 Refer to the documentation to see what this means
The minimum was found at the point 0.0,0.0
The value of the objective function at this point is 4.440892098500626e-16
The number of function evaluations was 1385警告をオフにすることは、何が起こっているかを気にしなくてもよいということではありません。様々なinform値の意味についてはドキュメントを参照する必要があります。
上記の例では、inform=2は、群れ内のすべての粒子の位置の標準偏差が設定された閾値(‘群れの標準偏差’)を下回っていることを意味します。これについて気にするかどうかは自由です。この例では、グローバル最小値を見つけたことがわかっているので、無視することにします
def ackley_ndim(_mode, x, objf, vecout, _nstate):
n = len(x)
sum1 = np.sum(x**2)
sum2 = np.sum(np.cos(2.0*np.pi*x))
objf = -20.0*np.exp(-0.2*np.sqrt(sum1/n)) - np.exp(sum2/n) + 20 + np.e
return objf, vecout# ソルバーを初期化する
options = {}
glopt.optset('Initialize = bnd_pso', options)
glopt.optset('Repeatability = ON', options)
glopt.optset('Seed = 1', options) # Could have used any integer
# N次元問題を設定する
dimensions = 200
bl = -5*np.ones(dimensions) # Lower bounds for each dimension
bu = 5*np.ones(dimensions) # Upper bounds for each dimension
# ソルバーを実行する
%timeit sol_x, fun_x, itt, inform = glopt.bnd_pso(bl, bu, ackley_ndim, options)9.39 s ± 65.6 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)