Fortran 数値計算入門

前へ   上へ   次へ

4 数値計算プログラムを自作する

このセクションでは自分で数値計算プログラムを書くという観点からいくつかの課題を取り上げます。

4.1 方程式の根を求める

数値計算プログラムの一例としてここでは方程式の根を求める問題（関数f(x)においてf(x)=0を満たすxを求める）を考えます。 線形方程式や低次（４次以下）の多項式は公式によりその根を求める事が可能ですが、多くの方程式はその厳密解を求めることが困難です。そのため数値計算により近似解を求める事が必要となります。

方程式の根を求める一つのシンプルな方法に２分法がありますがここではその２分法を取り上げます。 (この他にも定点法やニュートン法等があります）

２分法は初期値として下限と上限を与え、その範囲を狭めながら答えを見つける方法です。

例）

例えば以下の図に示される関数が与えられた場合の手順を説明します。

Step1
まず最初に初期値として f(a) と f(b) の符号が一致しないような下限と上限を設定します。 下記の例では下限を-2（①）、上限を0（④）に設定しています。

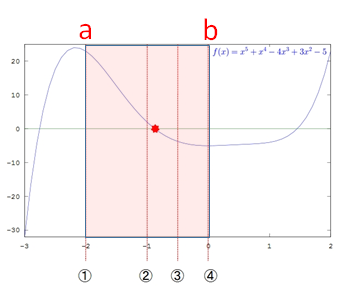
Step2
次に上限と下限の中間地点 m を求めます。
　m =(a + b) ÷ 2
　　= -1

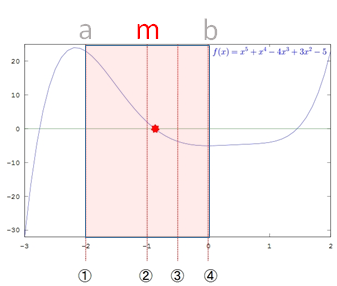
Step3
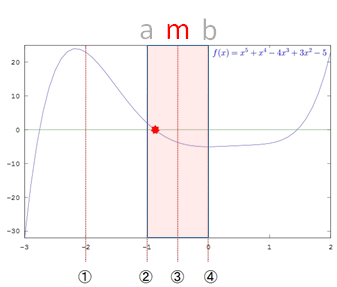
f(m)の符号とf(b)の符号が一致するかどうかを調べます。 符号が一致する場合は上限 b を m の地点まで下げて良いと判断します。 符号が一致しない場合は（f(a)とf(m)の符号が一致する事になるので）下限 a を m の地点まで上げて良いと判断します。
例）
　f(m) = f(-1) = 2
　f(b) = f(0) = -5
2と-5では符号が一致していないので下限 a を mの地点（②）まで移動させて、（今までの半分の大きさを持つ）新たな上下限とします。

その後の処理
Step2に戻り繰り返し処理を行います。そして a と b が適度に近づいた（|a-b|÷2<許容誤差）時点で計算を終了して、 (a+b)÷2を最終計算結果とします。

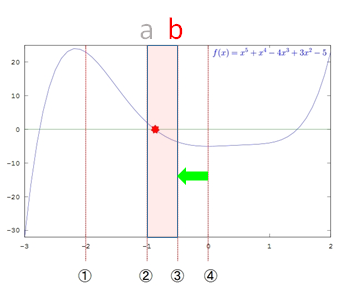
二分法の処理手順まとめ

• 初期値（下限=a、上限=b、許容誤差=e）を与える（ユーザー入力もしくは定数として）
• 繰り返し処理
  • 　下限と上限の中間（mとする）を求める
  • 　許容誤差内（abs(a-b)/2<e）ならば繰り返し処理を脱出
  • 　f(m) と f(b) の符号が同じならば b に m を代入、そうでなければ a に m を代入する（次の反復での上下限を設定）
    　符号が同じか判定する例1） if( f(m)>0 .and. f(b)>0 .or. f(m) <= 0 .and. f(b) <=0 ) then ...
    　符号が同じか判定する例2）if( f(m)>0 .eqv. f(b)>0 ) then ...
• mの値を結果として出力する

以下に上記の計算を行うプログラムコード例とその実行例を示します。

program bisection
  implicit none
  double precision m
  double precision :: a = -2d0    !　下限
  double precision :: b = 0d0     !  上限
  double precision :: e = 1d-10   !　許容誤差
  do
    m =(a+b)/2
    if( abs(a-b)/2 < e ) exit       !　許容誤差内なので計算終了(ループから抜け出す)
    if( f(m)>0 .eqv. f(b)>0 ) then  !　符号が同じかどうか判定している
      b = m
    else
      a = m
    end if
  end do
  print *, "Bisection result =", m   !　結果を出力
contains
  function f(x)
    double precision f, x
    f = x**5+x**4-4*x**3+3*x**2-5    ! 式を定義
  end function f
end program bisection


実行例：
 Bisection result =  -0.8714771153754555

4.1.1 ★ 演習課題：２分法を用いて２次方程式の根を求める

２分法を用いて以下の２次方程式の根を求めるプログラムを作成して下さい。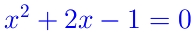

• 下限aの初期値は-3、上限bの初期値は0として計算を行って下さい。
• 許容誤差eは適当な値（例えば1d-10）として下さい。
• この例題は２次方程式ですので、解の公式により求めた答え（ -1±sqrt(2) ）も合わせて出力して下さい

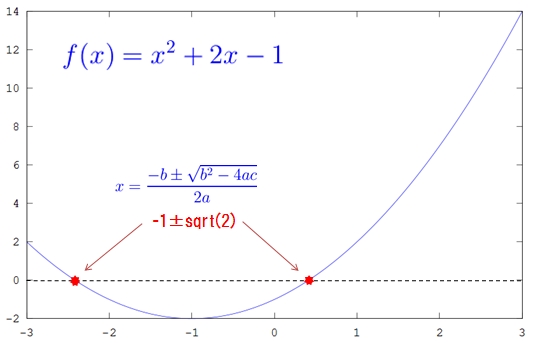
処理手順例

1. 適切な（f(a)とf(b)の符号が一致しない）上限と下限をaとbを設定する。
2. 許容誤差eを適当な値（1d-10等）に設定する。
3. 以下の３つのステップ（4.～6.）を繰り返す
4. aとbの真ん中のを求める。例：m=(a+b)/2
5. 許容誤差内ならば計算終了（|a-b|/2<e）
6. f(m)とf(b)の符号が同じならばbにmを設定する。もしそうでなければaにmを設定する
7. 結果(m)を出力する
8. 解の公式による結果を出力する

※関数としてf(x)は別途定義する。
式は以下のとおり：f = x**2 + 2*x - 1

実行例：
 Bisection result =  -2.4142135624133516
 Formula result   =  -2.4142135623730949   0.4142135623730952

[ bisection.f90 ] - ２分法により方程式の根を求めるプログラム例

4.2 台形則による積分を行う

数値計算の別の例としてここでは台形則を用いた積分を取り上げます。 台形則による積分とは、区間[a,b]においての関数の積分値を、 複数の台形面積の和を求めて近似する方法です。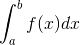

ここでは区間[1,2]における関数 f(x)=x**2 の積分値を求める例を取り上げます。

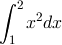
グラフで示すと以下のようになります。

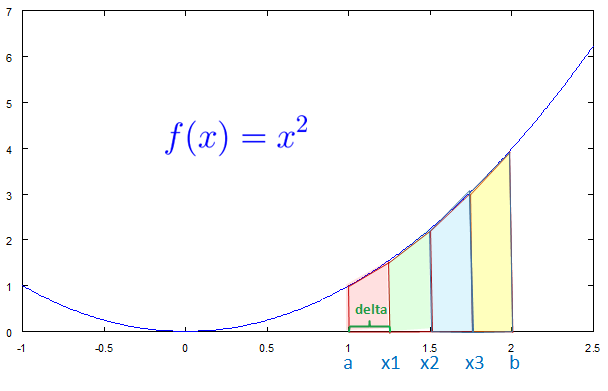
ここでは台形の数 n を 4 とした場合について説明します。 （積分値を4つの台形の面積の和で近似します。）

それぞれの台形（横を向いている）の高さ（ここではdeltaとします）は(b-a)/n で求めます。
　delta =(2-1) / n
　　　= 0.25

例えば、一番左の台形の面積は、台形の面積の公式をあてはめると、以下のとおりとなります。

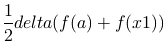
同様に4つすべての台形の面積を足すと以下のようになります。

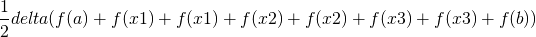
以下に台形則による積分を行い結果を表示するプログラムコード例、及びその出力結果例を示します。 （参考：解析的に求めた解は7/3 = 2.333333333...です。）

program trapezoidal_integration
  implicit none
  integer n, i
  double precision a, b, sum, delta, x1, x2
  a = 1d0     ! 下限
  b = 2d0     ! 上限
  n = 4       ! 台形の数
  sum = 0d0   ! f(X1) から f(Xn-1) までを足す
  delta =(b-a)/n
  do i = 1, n
    x1 = a+delta*(i-1)
    x2 = a+delta*i
    sum = sum + f(x1) + f(x2)
  end do
  print *, "Result =", sum * delta / 2
contains
  function f(x)
    double precision f, x
    f = x**2
  end function f
end program trapezoidal_integration


実行例：
 Result =   2.3437500000000000

4.2.1 ★ 演習課題：台形則を用いて積分値を求める

台形則を用いて以下を求めるプログラムを作成して下さい。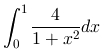

処理手順例

1. aとbをそれぞれ0（下限）と1（上限）に初期化する。
2. 台形の数であるnを適当な値（1000等）に設定する。
3. delta（台形の高さ）を初期化する。
   例）delta =(b-a)/n
4. sumを初期化する。
   例）sum = 0
5. ループ処理（do i=1, n）を行い、ステップ毎に各台形の上底と下底をsumに足し合わせて行く。 （掛け算とわり算はループ脱出後に行う）
   例）sum = sum + f(a+delta*(i-1)) + f(a+delta*i)
6. 以下の計算式で最終的な結果を出力する。
   　result = sum * delta / 2

※被積分関数としてf(x)は別途定義する。
式は以下のとおり：f = 4/(1+x**2)

実行例：
   3.1415924869231322

[ daikei.f90 ] - 台形則により積分値を求めるプログラム例

4.3 ガウスの消去法により連立一次方程式の解を求める

数値計算で良く必要となる連立一次方程式の解を求める例を取り上げます。 ここでは特にガウスの消去法として知られる方法を用いて連立一次方程式の解を求めます。

ガウスの消去法は大きく２つの処理フェーズに分けられます。

• 第一ステップ：変数を消去するステップ（前進消去(forward elimination)と呼ばれる）
• 第二ステップ：変数値を確定するステップ（後退代入(backward substitution)と呼ばれる）

ここでは以下の連立一次方程式を取り上げてガウスの消去法の処理手順を説明します。

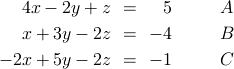
変数を消去するステップ

変数を消去するためにまずA式を用いてB式及びC式の x を消去することを考えます。 A式に両辺に適当な数（この例では1/4）を掛けてB式の x と同じ値にします。
※ここで1/4はB式のxの係数(=1)÷A式のxの係数(=4)となります。

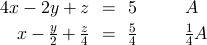
その後、B式から1/4を掛けたA式を引きます。

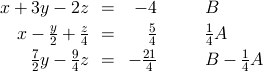
同様のやり方でC式から x を消去するためにC式からA式×(-2/4)を引きます。

以下にその結果を示します。B式、C式からxが消去されたことがわかります。

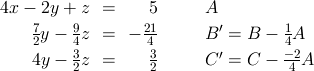
今度はB'式を用いてC'式から y を消去することを考えます。 B'式を用いてC'式から y を消去するためにはC'式からB'式×8/7を引きます。 8/7はC'式のyの係数(=4)÷B'式のyの係数=(7/2)を表しています。

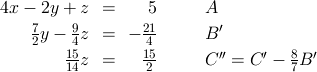
変数値を確定するステップ

上記までの処理で、C''式には変数 z のみが残っている状況となりました。 そこでここから順番にまずzを求め、次にB'式を用いてyを求め、 そして最後にA式を用いてxを求める事ができます。

ここではx=1, y=3, z=7が求まります。

4.3.1 プログラム例

以下に上記で説明したガウスの消去法を用いて連立一次方程式の解を求めるプログラム例を示します。 下記の例では以下の問題を解く例を示します。

通常このようなプログラムでは左辺の各係数を以下の図のように行列（係数のみが格納される）として取扱い、 右辺はベクトルとして取り扱います。上記式はそれぞれ下記のような行列AとベクトルBで表されます。

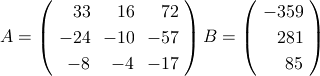
また下記のプログラムではこれらの行列A（左辺の係数）とベクトルB（右辺）と式の数をキーボードから入力するようになっています。 以下に入力可能なデータ例を示します。一番上の3は式が3つあることを示しています。 その次の３行は行列Aに与える係数で、最後の１行がベクトルBに与える右辺の値をそれぞれ示しています。

入力データ例：
3
33 16 72
-24 -10 -57
-8 -4 -17
-359 281 85

プログラムコード例

program gauss
  implicit none
  integer n, i, j, k
  double precision, allocatable :: a(:,:), b(:)
  double precision c, sum

  ! データを読み込む＆配列の領域確保
  read *, n
  allocate(a(n,n))
  allocate(b(n))
  read *,((a(i,j),j=1,n),i=1,n),(b(i),i=1,n)

  !前進消去(forward elimination)
  do k = 1, n - 1            ! 何番目の式を用いて変数を消去するか（上から順番にn-1番目の式まで）
    do i = k + 1, n          ! 変数が消去される側の式（k+1番目からn番目の式まで）
      c = a(i,k)/a(k,k)      ! 係数の大きさを合わせるための比率を計算しておく
      do j = k + 1, n        ! i番目の式からc倍したk番目の式を引いて変数を消去する
        a(i,j) = a(i,j) - c*a(k,j)
      end do
      b(i) = b(i) - c*b(k)   ! i番目の右辺からもc倍したk番目の右辺を引く
    end do
  end do

  !後退代入(backward substitution)
  b(n) = b(n)/a(n,n)          ! 一番最後の変数（ここではz）の解を求めb(n)に格納する
  do i = n - 1, 1, -1         ! 順番にその他の変数の解を求めてb(i)に格納する
    sum = 0.0d0
    do k = i + 1, n
      sum = sum + a(i,k)*b(k)
    end do
    b(i) =(b(i)-sum)/a(i,i)
  end do

  !結果を出力
  print *
  print *, "Solution"
  print "((f9.4))", b

end program gauss

[ gauss.f90 ] - ガウスの消去法プログラム例

実行例：
3
33 16 72
-24 -10 -57
-8 -4 -17
-359 281 85

 Solution
   1.0000
  -2.0000
  -5.0000

4.3.2 部分ピボット選択による改良

上記までに説明した方法には実は少し問題があります。 例えば以下のような連立方程式を考えます。

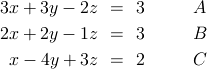
上記で説明した手順通りA式を用いてB式とC式からxを消去することを考えます。 A式を用いてB式から x を消去するにはB式からA式×2/3を引きます。 同様にC式から x を消去するにはC式からA式×1/3を引きます。 すると以下のような結果が得られます。

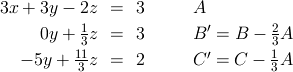
ここでB'式も0yとなりyが消去されてしまっていることに注目して下さい。 このまま計算を続けようとしますと0で割り算を行う事になってしまいます。 また0ではない場合でも係数の絶対値が非常に小さくなった場合にはオーバーフローや大きな誤差の原因となります。 このような不都合を防ぐために残りの式の順番を入れ替えて計算を行う方法が部分ピボット選択の考え方です。

今までは上の式から順番により下の式の変数を消去する方法をとってきましたが、 部分ピボット選択の考え方では残りの式の順番を入れ替えて、 その時点で消去したい変数の係数の絶対値が一番大きな式を利用するようにします。 これにより上述の0で割り算する問題が解決する他、 係数の絶対値が非常に小さな値になってしまった場合に発生する誤差の問題も合わせて解決されます。

以下に部分ピボット選択部分のコードセグメントを示します。

!前進消去(forward elimination)
do k = 1, n - 1
  l = k
  do i = k+1, n   ! 残りの式から消去しようとしている変数の絶対値が一番大きな式を探す
    if( abs(a(l,k)) < abs(a(i,k)) ) then   ! 式lと式iの係数絶対値の比較
      l = i
    end if
  end do
  if( l .ne. k ) then   ! 現在の式（k）よりも係数が大きい式（l）が見つかったので係数及び右辺を交換
    tmp = a(l,:)
    a(l,:) = a(k,:)
    a(k,:) = tmp
    tmp(1) = b(l)
    b(l) = b(k)
    b(k) = tmp(1)
  endif
  ...
end do

最後に部分ピボット選択を取り入れた完結コードを以下に示します。

[ gaussPivot.f90 ] - 部分ピボット選択付きガウスの消去法プログラム例


前へ   上へ   次へ