より高速なデータフィッティングソルバー

新しい非線形最小二乗法（NLN-LSQ）信頼領域ソルバー

複雑な数値モデルのパラメータを実世界の観測値に適合させるためにキャリブレートすることは、金融、物理学、シミュレーション、エンジニアリングなどの業界で見られる最も一般的な問題の一つです。nAGではnAGライブラリのMark 27.1にて、様々なアルゴリズムと正則化技術を実装した、制約のない拘束されたフィッティング問題および拘束されたフィッティング問題のための新しい非線形最小二乗法（NLN-LSQ）信頼領域ソルバー handle_solve_bxnl $e04gg$を紹介しています。以下の形式の小～中規模のフィッティング問題（パラメータ数千個程度まで）を対象としています。

$$\begin{array}{llll}\hfill \underset{x\in R^n}{\text{minimize}}& {\displaystyle \sum _{i=1}^m{\left(\phi \left(t_i,x\right)-y_i\right)}^2}& \hfill & \\ \hfill \text{subject to}& l\leqq x\leqq u,& \hfill & \end{array}$$

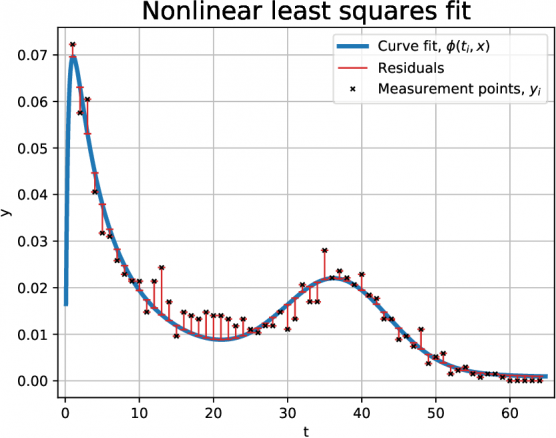
ここでの考え方は、m 個の観測されたデータ・ポイント $\left(t_i,y_i\right)$ $黒い点$に適合する平滑関数 $\phi \left(t,x\right)$ $青い線$で表されるモデルのパラメー タ $x$ の最適値を見つけることです。つまり、モデルとデータの間の二乗誤差を最小化することです（垂直の赤いバー）。 e04ggはnAGライブラリ内の現在の非線形最小二乗ソルバーよりも大幅に改善されています。さらに、このソルバーは lsq_uncon_quasi_deriv_comp (e04gb)のような制約のないソルバーと、lsq_gencon_deriv (e04us) のような完全に制約のあるソルバーの間のギャップを埋めるものです。 e04ggはnAG最適化モデリングスイートの一部であり、スイート内のソルバーのインターフェースの明確さと一貫性を提供します。 この新しいソルバーはRutherford Appleton Laboratory [1]との共同研究から生まれたもので、数学的最適化における提供物の拡大と改善のためのnAGの継続的な努力を実証しています。

handle_solve_bxnl $e04gg$の特徴

• 確立された手法であるトラスト領域法を利用。Powell's dogle法やGauss-Newton法などの単純な手法から、収束の難しさを克服したより洗練されたTensor-Newton法まで、様々なアルゴリズムが実装されている。
• 問題定式化と信頼領域部分問題の両方に異なるタイプの正則化を組み込むことで、データのオーバーフィットを回避。
• 与えられたポイントで関数φ$t,x$やその勾配を評価できない場合に回復する能力。
• オプションの残差重みを使用して観測データの不確実性を説明。
• 問題とデータの許容範囲に適合できる柔軟な停止基準。

e04gbおよびe04usの最新の代替品

新しいソルバーe04ggは、ライブラリ内の従来ルーチン、つまり制約のない非線形最小二乗問題の場合はe04gb、単純な変数境界の問題の場合はe04us、に比べて、前例のない堅牢性と大幅な高速化を実現しています。 新しいソルバーにアップグレードすることを強くお勧めします。

68 の制約のない非線形最小二乗 CUTEst 問題について，e04gg と e04gb を比較したベンチマークを以下に示します。 3つのプロットは、新しいソルバーが高速であることを示しています。 （a）が示す通り、60% の問題をより短い時間で解いており、よりロバストで、25%の多くの問題を解いています。 （b）では、必要なユーザコールバックが少ない事が示されています。（55%の問題では関数呼び出しが少ない） （c）は、勾配評価回数が示されています。（65%の問題で勾配評価が少ない）

e04gbソルバーは単純境界を直接扱うように設計されていないので、このような問題には通常e04usが使用されます。しかし、より一般的なソルバーであるe04usは、単純境界の存在下ではe04ggのようにNLN-LSQ問題の構造を完全に利用することはできません。これが、45%の問題で高速化が見られる理由です。（d） 112の非制約および境界制約のある非線形最小二乗CUTEst問題についてe04usとe04ggを比較すると、65%の問題で関数と勾配の呼び出しが少なくて済んでいる事がわかります。（eとf）

以下の図の説明：（a）–（c）は68個の CUTEstの制約なし非線形最小二乗問題でソルバーe04ggとe04gbを比較したパフォーマンスプロファイルで、（d）–（f）は、112個のCUTEstの制約なしおよび境界制約付き非線形のe04ggとe04usのパフォーマンスプロファイルを示します。パフォーマンス測定値は、秒単位の時間（aおよびd）、関数呼び出しの数（bおよびe）、および勾配呼び出しの数（cおよびf）です。時間プロットにおいては、高い線はより高速なソルバーを示します。関数呼び出し回数と勾配呼び出し回数のプロットにおいては、高い線の方が少ない回数である事を示します。

（a）時間: e04gbとe04ggの比較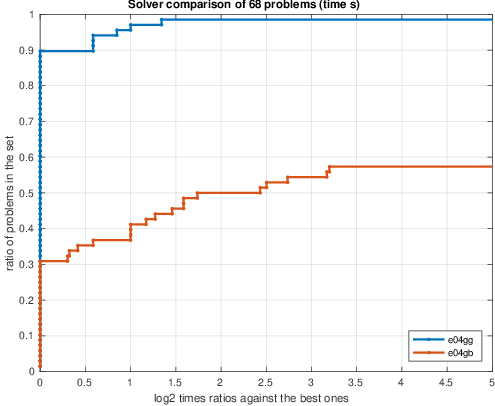

（b）関数評価回数: e04gbとe04ggの比較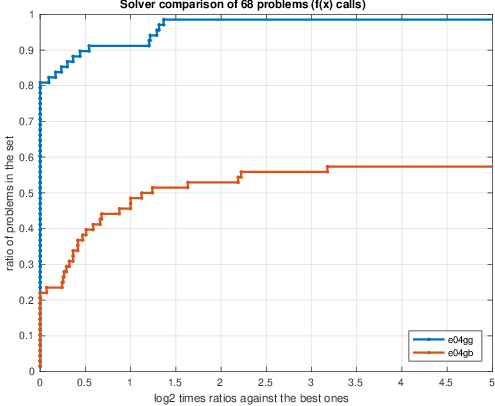

（c）勾配評価回数: e04gbとe04ggの比較

（d）時間: e04usとe04ggの比較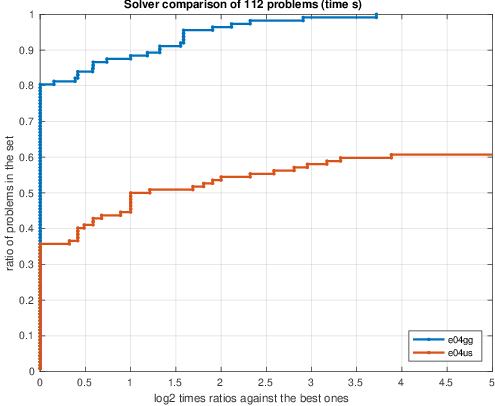

（e）関数評価回数: e04usとe04ggの比較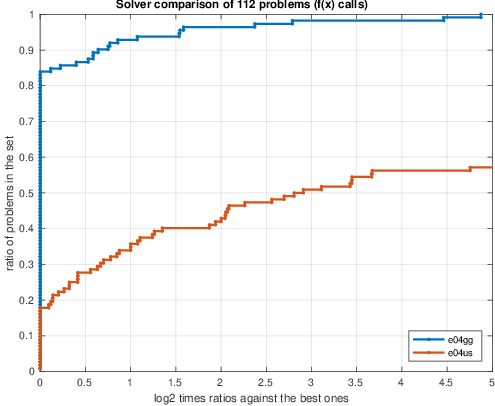

（f）勾配評価回数: e04usとe04ggの比較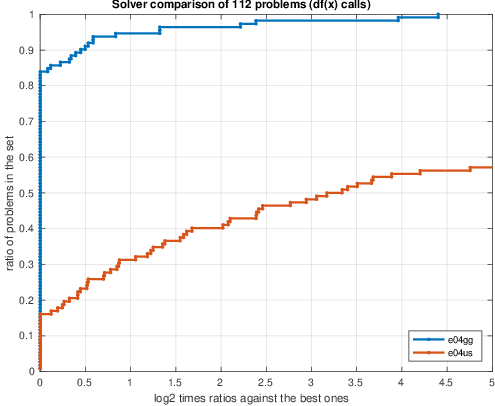

実際の例：パーティクルトラックのデータフィッティング

次の例は、PADCエッチングされた核トラックデータを複雑な分布に適合させるためのe04ggの使用法を示しています。 ターゲットシートがスキャンされ、トラックの直径（図の左側の画像の赤いくさび）がヒストグラム（図の右側のプロットの青いバー）に記録され、正規モデルと対数正規混合モデルが得られた実験に適合されます。

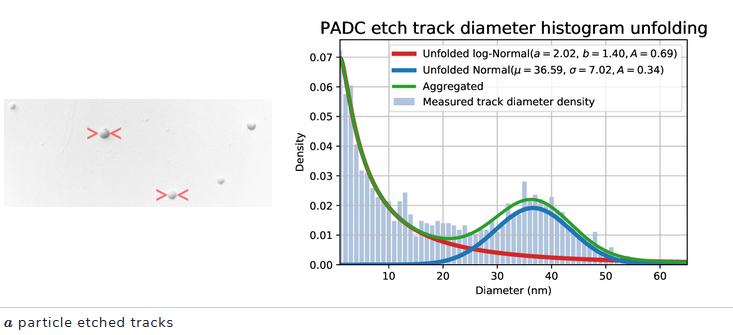
e04ggは、ヒストグラムの高さを使用して6つのパラメーターモデル（以下）を適合させるために使用されます。

$$\begin{array}{llll}\hfill \phi \left(\right.t,x=\left(u,s,A_g,a,b,A_l\right)\left)\right.& =\text{Normal}\left(u,s,A_g\right)+\text{log-Normal}\left(a,b,A_l\right)& \hfill & \\ \hfill \text{subject to}& 0=x,& \hfill & \end{array}$$

正則化と残差重みの使用により、e04ggは2つの分布のパラメータを展開するためのロバストな解 x* を提供しました（右プロットの赤と青の曲線）。これらを足し合わせると、緑の曲線が得られ、これがフィッティングに使用されます。この例のデータと完全なPythonソースコードはこちらから入手できます。

リファレンス

[1]   Gould N I M, Rees T, and Scott J A $2017$ A higher order method for solving nonlinear least-squares problems. Technical report, RAL-P-1027-010 RAL Library. STFC Rutherford Appleton Laboratory. レポートへのリンク.

[2]   Kanzow C, Yamashita N, and Fukushima M $2004$ Levenberg-Marquardt methods with strong local convergence properties for solving nonlinear equations with convex constraints. Journal of Computational and Applied Mathematics 174 375-397.

[3]   Sajo-Bohus L. $2020$ Data provided in private communication.