複雑な数値モデルの最適化は、業界で見られる最も一般的な問題の1つです（金融、マルチフィジックスシミュレーション、エンジニアリングなど）。 ガウス-ニュートン（非線形最小二乗構造の問題の場合）やCG（非構造化非線形目的の場合）などの標準最適化アルゴリズムを使用してこれらの最適化問題を解決するには、モデルの導関数を適切に推定する必要があります。 それらは次の方法で計算できます。
- 明示的に書かれた導関数
- 自動微分(nAG AD tools)
- 有限差分 （bumping）
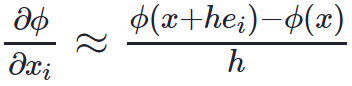
正確な導関数を計算するのが簡単な場合は、導関数ベースの方法を使用することをお勧めします。 ただし、モデルがブラックボックスの場合、導関数を明示的に記述したり、ADメソッドを適用したりすることは不可能な場合があります。 有限差分を介して導関数を推定する代替案は、以下に示すようないくつかの問題があるため、すぐに非現実的または計算コストが高くなりすぎる可能性があります。
- 計算コストが高い, 1つの勾配評価に、少なくとも（n+1）回のモデル評価が必要です。。
- 不正確モデルの摂動（h）のサイズは、微分推定の品質に大きく影響し、選択するのは簡単ではありません。
- ノイズに敏感モデルが何らかのランダム性（モンテカルロシミュレーションなど）の影響を受ける場合、または計算時間を節約するために低精度で計算される場合、有限差分推定は非常に不正確になります。
- モデル評価の利用率が低い各評価は1つの勾配の1つの要素にのみ使用され、その勾配がソルバーにとって役に立たなくなるとすぐに情報が破棄されます。
これらの問題は、最適化ソルバーの収束を大幅に遅くしたり、完全に妨げたりする可能性があります。 逆に、DFOソルバーは、これらの状況下でも適切な計算が行われるように設計されていて、はるかに少ない関数評価で収束に達することができ、モデル評価のノイズに対して非常に堅牢です。
nAGはMark 27で非線形最小二乗問題のモデルベースDFOソルバ nag_opt_handle_solve_dfls (e04ff) と nag_opt_handle_solve_dfls_rcomm (e04fg) 及び非構造化非線形問題のモデルベースDFOソルバ nag_opt_handle_solve_dfno (e04jd) と nag_opt_handle_solve_dfno_rcomm (e04je) を発表しました。これらのソルバーには以下に示すような魅力的な特徴があります。
- パフォーマンスの向上
- シンプルなインターフェースでnAG最適化モデリングスイートに統合
- 逆通信インターフェースも利用可能 (e04fg, e04je);
- 最小で２回の評価で計算進展
- ノイズに対する回復力の向上
問題の構造
実際によくある問題の1つは、実世界の観測に可能な限りフィットするようにモデルのパラメータをチューニングすることです。i=1,2,...,m の間、時刻 ti で観測され、結果 yi で測定されたプロセスを考えてみましょう。さらに、プロセスは数値モデルφt,xに従って動作すると仮定します。測定値が不正確でプロセスがモデルに正確に追従していないかもしれないという事実を考えると、測定値へのモデルの適合の誤差が最小化されるようにモデル・パラメータ x を見つけることは有益です。これは、x が決定変数であり、目的関数が各測定における適合の二乗誤差の和である最適化問題として定式化することができます。
minimizex∈Rn∑mi=1(φ(ti,x)-yi)2subject tol≦x≦u
最適化問題が非線形最小二乗として書けない場合は、より一般的な定式化を使用する必要があります。
minimizex∈Rnf(x)subject tol≦x≦u
ノイズロバスト性
εが区間[-ν,ν]のランダムな一様ノイズであり、riがローゼンブロック検定関数の残差である、以下の非拘束問題を考えてみましょう。
minimizex∈Rnf(x)=m∑i=1(ri(x)+ε)2
この問題を有限差分と組み合わせたガウス・ニュートン法、 nag_opt_lsq_uncon_mod_func_comp (e04fc) 及び対応するDFOソルバー (e04ff)を用いて解いてみましょう。以下に示す様々なノイズレベルνに対して
f(x)<max(10−8,10×ν2)
「達成可能な」精度を持つ解を見つけるために必要なモデル評価の数を以下（表１）に示します。
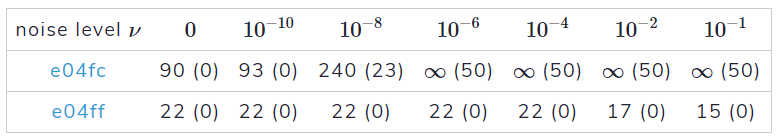
表1の数字は、問題を解くための評価数の平均（50回の実行で）を示している。括弧内の数字は、50回の実行のうち失敗した回数を示す。
この例では、新しいDFOソルバーはモデル評価の点で安価であり、且つノイズに対してはるかにロバストであることがわかります。