nAGライブラリの高速インプライドボラティリティ

1. はじめに

金融工学の世界において、インプライドボラティリティの計算は極めて重要な役割を果たしています。特に、高頻度取引やリスク管理において、大量のデータに対して高速かつ正確な計算が求められています。この課題に対して、nAGライブラリの最新版（Mark 27.1）は革新的なソリューションを提供しています。

2. ヨーロピアンオプションのインプライド・ボラティリティ

2.1 理論的背景

ブラック・ショールズ方程式は、ヨーロピアンコールオプションの価格を以下のように定義しています：

$$C = S_0 \Phi \left( \frac {\ln \left( \frac {S_0}{K} \right) + \left[ r + \frac {\sigma^2}{2} \right] T}{\sigma \sqrt {T}} \right) - Ke^{-rT} \Phi \left( \frac {\ln \left( \frac {S_0}{K} \right) + \left[ r - \frac {\sigma^2}{2} \right] T}{\sigma \sqrt {T}} \right)$$

ここで： - T：契約の満期までの時間 - S₀：原資産のスポット価格 - K：オプションの行使価格 - r：無リスク金利 - σ：ボラティリティ

インプライドボラティリティ（σ）は、この方程式からσを求める計算によって得られますが、直接的な解法は存在しません。そのため、高度な数値計算手法が必要となります。

2.2 ボラティリティ・サーフェイスの複雑性

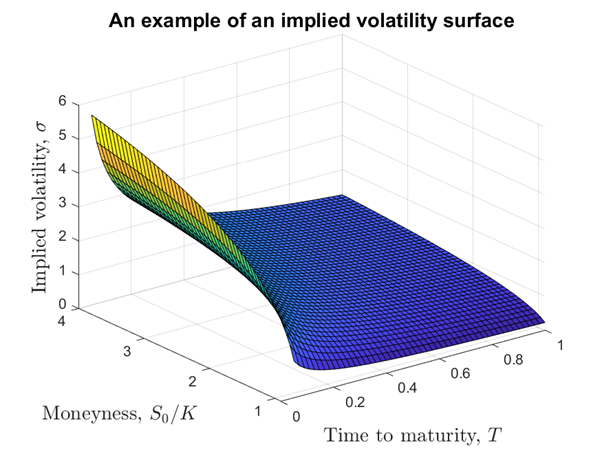
上図が示すように、ボラティリティ・サーフェイス（価格や満期までの時間によってボラティリティがどのように変化するかを三次元的にプロットしたもの）は非常に複雑な形状を持つことがあります。この複雑性が、インプライドボラティリティの計算を困難にしている主な要因の一つです。

3. nAGライブラリの革新的アプローチ

nAGライブラリのMark 27.1版に含まれる新ルーチンs30acfは、この課題に対する画期的なソリューションを提供します。

3.1 二つの先進的アルゴリズム

3.1.1 Jackel $2015$ の手法

• 特徴: 3次Householder法を使用
• 精度: 最も極端な入力を除き、ほぼすべての入力に対して機械精度に近い精度を達成
• 適用: 短いデータベクトルに対して特に高速

3.1.2 Glau et al. $2018$ のアルゴリズム

• 特徴: チェビシェフ補間を使用
• 最適化: nAGとロンドンのクイーン・メアリー大学の数学者との共同研究による性能強化
• 設計: 長いデータベクトルに対して最適化され、ベクトル命令を効率的に利用
• 柔軟性: 近似精度を調整可能（単精度相当の高速モードあり）

3.2 技術的詳細

チェビシェフ法の概要（Glau et al., 2018より）

1. 正規化ブラック・ショールズ価格: インプライドボラティリティの計算を二変数問題（moneyness xと時間スケール調整済みボラティリティv）に簡略化。

   $$c(x, v) = e^{x/2} \Phi\left(\frac{x}{v} + \frac{v}{2}\right) - e^{-x/2} \Phi\left(\frac{x}{v} - \frac{v}{2}\right)$$

2. チェビシェフ補間: インプライドボラティリティ関数 v$x, c$ を二変数チェビシェフ多項式で近似。

   $$v(x, c) \approx I_N(x, c) = \sum_{i=0}^{N_1} \sum_{j=0}^{N_2} a_{ij} T_i(x) T_j(c)$$

3. 領域分割とスケーリング: 低・中・高ボラティリティ領域で異なるスケーリング関数を適用し、精度を向上。

4. サブ指数的誤差減衰: 理論的に証明された高精度な近似が可能。

Jackel $2015$ の手法の要点

1. 4分岐初期推定: log-moneyness xに応じて4つの有理関数分岐を使用。

2. 非線形変換: 入力価格の非線形変換を適用し、推定精度を向上。

3. Householder法: 4次収束のHouseholder法を使用し、高速かつ高精度な反復を実現。

4. nAGライブラリの優位性

4.1 高速性と精度のバランス

nAGライブラリの新しいルーチンは、高速性と精度のバランスを追求しています。Jackel $2015$の手法は、極めて高い精度を実現しながらも、短いデータベクトルに対して高速な計算を可能にします。一方、Glau et al. $2018$のアルゴリズムは、長いデータベクトルに対して最適化されており、ベクトル命令を効率的に利用することで高速な処理を実現します。

4.2 柔軟性と適応性

nAGライブラリの手法は、ユーザーのニーズに応じて精度と速度のトレードオフを調整できる柔軟性を持っています。特に、Glau et al.のアルゴリズムでは、単精度相当の高速モードも提供されており、ユーザーは用途に応じて最適な設定を選択できます。

4.3 堅牢性と信頼性

nAGは50年以上にわたり数値計算ライブラリを開発してきた実績があり、その品質と信頼性は業界で高く評価されています。新しいインプライドボラティリティ計算ルーチンも、この長年の経験と専門知識に基づいて開発されています。

5. 応用例

5.1 高頻度取引への応用

nAGライブラリの高速・高精度なインプライドボラティリティ計算は、ミリ秒単位の反応が求められる高頻度取引において大きな優位性をもたらします。特に、大量のオプションデータをリアルタイムで処理する必要がある場合に威力を発揮します。

5.2 リスク管理と規制対応

金融機関は、規制要件（例：バーゼルIII）に対応するため、大規模なポートフォリオに対して迅速かつ正確なリスク計算を行う必要があります。nAGライブラリの効率的なアルゴリズムは、この要求に応えるソリューションとなります。

5.3 モデルキャリブレーション

より複雑な確率的ボラティリティモデル（例：Heston模型）のキャリブレーションにおいて、高速なインプライドボラティリティ計算は計算時間を大幅に削減し、より精緻なモデリングを可能にします。

関連情報:

• ノイズに強いDFO：従来手法との比較と優位性
• DFOによる、Heston モデルのキャリブレーション高速化

6. 結論

nAGライブラリの新しいインプライドボラティリティ計算ルーチンは、金融工学における計算上の重要な課題に対する効率的なソリューションを提供しています。

参考文献

1. Jackel, P. $2015$. Let’s be rational. Wilmott, 2015$75$, 40-53.
2. Glau, K., Herold, P., Madan, D. B., & Pötz, C. $2018$. The Chebyshev method for the implied volatility. Accepted for publication in the Journal of Computational Finance.