Keyword: 多変量時系列, 多入力モデル, 推定
概要
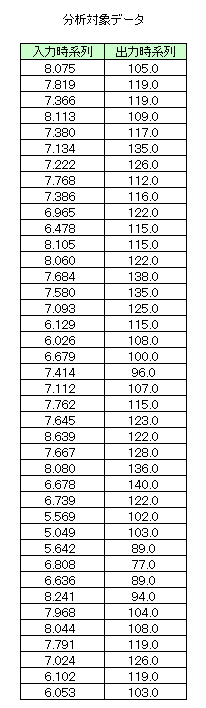
本サンプルは時系列モデルの推定の計算を行うC言語によるサンプルプログラムです。 本サンプルは以下に示される時系列データを分析し、時系列モデルの推定値を出力します。
※本サンプルはnAG Cライブラリに含まれる関数 nag_tsa_multi_inp_model_estim() のExampleコードです。本サンプル及び関数の詳細情報は nag_tsa_multi_inp_model_estim のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本関数の詳細はnag_tsa_multi_inp_model_estim のマニュアルページを参照)| このデータをダウンロード |
nag_tsa_multi_inp_model_estim (g13bec) Example Program Data
40 2 20
1 0 0 0 0 1 4
1
0
1
3
0.0 0.0 2.0 0.5 0.0
8.075 105.0
7.819 119.0
7.366 119.0
8.113 109.0
7.380 117.0
7.134 135.0
7.222 126.0
7.768 112.0
7.386 116.0
6.965 122.0
6.478 115.0
8.105 115.0
8.060 122.0
7.684 138.0
7.580 135.0
7.093 125.0
6.129 115.0
6.026 108.0
6.679 100.0
7.414 96.0
7.112 107.0
7.762 115.0
7.645 123.0
8.639 122.0
7.667 128.0
8.080 136.0
6.678 140.0
6.739 122.0
5.569 102.0
5.049 103.0
5.642 89.0
6.808 77.0
6.636 89.0
8.241 94.0
7.968 104.0
8.044 108.0
7.791 119.0
7.024 126.0
6.102 119.0
6.053 103.0
- 1行目はタイトル行で読み飛ばされます。
- 2行目に時系列データの数(nxxy)、入力時系列、出力時系列の合計数(nseries)、最大反復数(max_iter)を指定しています。
- 3行目はARIMAモデルの次数ベクトル(自己回帰の数p、非季節階差の次数d、移動平均q、季節自己回帰bigp、季節階差の次数bigd、季節移動平均bigqと季節期間s)を指定しています。
- 4〜7行目は伝達関数モデルの次数(transfv)を指定しています。
- 8行目は多入力モデルの引数(para)を指定しています。
- 9〜48行目に入力時系列と出力時系列の値(xxy)を指定しています。
出力結果
(本関数の詳細はnag_tsa_multi_inp_model_estim のマニュアルページを参照)| この出力例をダウンロード |
nag_tsa_multi_inp_model_estim (g13bec) Example Program Results
Parameters to g13bec
____________________
nseries...................... 2
criteria............ Nag_Marginal cfixed................. Nag_FALSE
alpha.................. 1.00e-02 beta................... 1.00e+01
delta.................. 1.00e+03 gamma.................. 1.00e-07
print_level... Nag_Soln_Iter_Full
outfile................ stdout
Iter = -1 Residual = 6.456655e+03 Objf = 7.097184e+03
phi 0.000000e+00
stheta 0.000000e+00
omega series 1 2.000000e+00
delta series 1 5.000000e-01
constant 8.688399e+01
Iter = 0 Residual = 5.802775e+03 Objf = 6.378435e+03
phi 0.000000e+00
stheta 0.000000e+00
omega series 1 2.000000e+00
delta series 1 5.000000e-01
constant 8.573272e+01
Iter = 1 Residual = 2.354664e+03 Objf = 2.498647e+03
phi 6.589153e-01
stheta 6.571389e-02
omega series 1 3.721182e+00
delta series 1 5.237968e-01
constant 5.739128e+01
Iter = 2 Residual = 1.922339e+03 Objf = 2.032375e+03
phi 6.417690e-01
stheta -2.361191e-01
omega series 1 4.523132e+00
delta series 1 5.742824e-01
constant 3.814856e+01
Iter = 3 Residual = 1.530797e+03 Objf = 1.630603e+03
phi 5.550797e-01
stheta -3.097333e-01
omega series 1 7.697297e+00
delta series 1 7.358370e-01
constant -9.322197e+01
Iter = 4 Residual = 1.232926e+03 Objf = 1.324116e+03
phi 3.698329e-01
stheta -2.145294e-01
omega series 1 9.116523e+00
delta series 1 6.923742e-01
constant -9.985550e+01
Iter = 5 Residual = 1.200813e+03 Objf = 1.289272e+03
phi 3.889281e-01
stheta -2.649652e-01
omega series 1 8.906746e+00
delta series 1 6.659905e-01
constant -7.782515e+01
Iter = 6 Residual = 1.197922e+03 Objf = 1.286734e+03
phi 3.752731e-01
stheta -2.499956e-01
omega series 1 8.957172e+00
delta series 1 6.616140e-01
constant -7.656262e+01
Iter = 7 Residual = 1.197934e+03 Objf = 1.286623e+03
phi 3.804046e-01
stheta -2.594526e-01
omega series 1 8.954182e+00
delta series 1 6.599012e-01
constant -7.553429e+01
Iter = 8 Residual = 1.198009e+03 Objf = 1.286613e+03
phi 3.807082e-01
stheta -2.567453e-01
omega series 1 8.956063e+00
delta series 1 6.597438e-01
constant -7.549190e+01
Iter = 9 Residual = 1.197988e+03 Objf = 1.286612e+03
phi 3.808772e-01
stheta -2.580559e-01
omega series 1 8.955983e+00
delta series 1 6.596508e-01
constant -7.543851e+01
Iter = 10 Residual = 1.198002e+03 Objf = 1.286611e+03
phi 3.809218e-01
stheta -2.575832e-01
omega series 1 8.956106e+00
delta series 1 6.596484e-01
constant -7.544005e+01
Iter = 11 Residual = 1.197997e+03 Objf = 1.286611e+03
phi 3.809235e-01
stheta -2.577863e-01
omega series 1 8.956084e+00
delta series 1 6.596411e-01
constant -7.543552e+01
The number of iterations carried out is 11
The final values of the parameters and their standard deviations are
i para[i] sd
1 0.380924 0.166379
2 -0.257786 0.178178
3 8.956084 0.948061
4 0.659641 0.060239
5 -75.435521 33.505341
The residual sum of squares = 1.197997e+03
The objective function = 1.286611e+03
The degrees of freedom = 34.00
The correlation matrix is
1.0000 -0.1839 -0.1775 -0.0340 0.1394
-0.1839 1.0000 0.0518 0.2547 -0.2860
-0.1775 0.0518 1.0000 -0.3070 -0.2926
-0.0340 0.2547 -0.3070 1.0000 -0.8185
0.1394 -0.2860 -0.2926 -0.8185 1.0000
The residuals and the z and n values are
i res[i] z(t) noise(t)
1 0.397 180.567 -75.567
2 3.086 191.430 -72.430
3 -2.818 196.302 -77.302
4 -9.941 195.460 -86.460
5 -5.061 201.594 -84.594
6 14.053 199.076 -64.076
7 2.624 195.211 -69.211
8 -5.823 193.450 -81.450
9 -2.147 197.179 -81.179
10 -0.216 196.217 -74.217
11 -2.517 191.812 -76.812
12 7.916 184.544 -69.544
13 1.423 194.322 -72.322
14 11.936 200.369 -62.369
15 5.117 200.990 -65.990
16 -5.672 200.468 -75.468
17 -5.681 195.763 -80.763
18 -1.637 184.025 -76.025
19 -1.019 175.360 -75.360
20 -2.623 175.492 -79.492
21 3.283 182.162 -75.162
22 6.896 183.857 -68.857
23 5.395 190.797 -67.797
24 0.875 194.327 -72.327
25 -4.153 205.558 -77.558
26 6.206 204.261 -68.261
27 4.208 207.104 -67.104
28 -2.387 196.423 -74.423
29 -11.803 189.924 -87.924
30 6.435 175.158 -72.158
31 1.342 160.761 -71.761
32 -4.924 156.575 -79.575
33 4.799 164.256 -75.256
34 -0.074 167.783 -73.783
35 -6.023 184.483 -80.483
36 -6.427 193.055 -85.055
37 -2.527 199.390 -80.390
38 2.039 201.302 -75.302
39 0.243 195.695 -76.695
40 -3.166 183.738 -80.738
- 6行目に適用されている時系列の数が出力されています。
- 8〜12行目には以下に示すプログラムのオプション引数が出力されています。
criteria 推定基準の尤度オプション。"Nag_Marginal"は周辺尤度を意味します。 cfixed 定数 c を初期値に固定されたままにするか推定するかを指定します。"Nag_FALSE"は推定されることを意味します。 alpha 検索処理の大きさを抑制するのに使用される値。 beta alphaの値を調節する乗数。 delta 定常性や変換性のテストの許容値。 gamma 収束基準。 print_level 結果出力のレベル。"Nag_Soln_Iter_Full"は配列パラメータの各引数の説明と値が出力されることを意味します。 outfile 結果が出力されるファイル名。 - 14〜116行目には各反復ごとの残差、目的関数値、ファイ、シータ、オメガ、デルタ、定数が出力されています。
- 120行目には実行した反復数が出力されています。
- 122〜129行目にはパラメータの最終値と標準偏差が出力されています。
- 132行目には残差平方和が出力されています。
- 134行目には目的関数値が出力されています。
- 136行目には自由度が出力されています。
- 138から144行目には相関行列が出力されています。
- 146〜189行目には残差、Z値、ノイズが出力されています。
ソースコード
(本関数の詳細はnag_tsa_multi_inp_model_estim のマニュアルページを参照)
※本サンプルソースコードはnAG数値計算ライブラリ(Windows, Linux, MAC等に対応)の関数を呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
/* nag_tsa_multi_inp_model_estim (g13bec) Example Program.
*
* CLL6I261D/CLL6I261DL Version.
*
* Copyright 2017 Numerical Algorithms Group.
*
* Mark 26.1, 2017.
*/
#include <nag.h>
#include <stdio.h>
#include <string.h>
#include <nag_string.h>
#include <nag_stdlib.h>
#include <nagg13.h>
#define XXY(I, J) xxy[(I) *tdxxy + J]
int main(void)
{
Integer exit_status = 0;
Integer i, inser, j, npara, nseries, nxxy, tdxxy;
Nag_ArimaOrder arimav;
Nag_G13_Opt options;
Nag_TransfOrder transfv;
double df, objf, *para = 0, rss, *sd = 0, *xxy = 0;
NagError fail;
INIT_FAIL(fail);
printf("nag_tsa_multi_inp_model_estim (g13bec) Example Program Results\n");
scanf(" %*[^\n]"); /* Skip heading in data file */
#define CM(I, J) options.cm[(J)+(I) *options.tdcm]
#define ZT(I, J) options.zt[(J)+(I) *options.tdzt]
/*
* Initialize the option structure.
*/
/* nag_tsa_options_init (g13bxc).
* Initialization function for option setting
*/
nag_tsa_options_init(&options);
scanf("%ld%ld%ld", &nxxy, &nseries,
&options.max_iter);
if (nxxy > 0 && nseries > 0) {
/*
* Set some specific option variables to the desired values.
*/
options.criteria = Nag_Marginal;
options.print_level = Nag_Soln_Iter_Full;
/*
* Allocate memory to the arrays in structure transfv containing
* the transfer function model orders of the input series.
*/
/* nag_tsa_transf_orders (g13byc), see above. */
nag_tsa_transf_orders(nseries, &transfv, &fail);
/*
* Read the orders vector of the ARIMA model for the output noise
* component into structure arimav.
*/
scanf("%ld%ld%ld%ld%ld"
"%ld%ld", &arimav.p, &arimav.d, &arimav.q,
&arimav.bigp, &arimav.bigd, &arimav.bigq, &arimav.s);
/*
* Read the transfer function model orders of the input series into
* structure transfv.
*/
inser = nseries - 1;
for (j = 0; j < inser; ++j)
scanf("%ld", &transfv.b[j]);
for (j = 0; j < inser; ++j)
scanf("%ld", &transfv.q[j]);
for (j = 0; j < inser; ++j)
scanf("%ld", &transfv.p[j]);
for (j = 0; j < inser; ++j)
scanf("%ld", &transfv.r[j]);
npara = 0;
for (i = 0; i < inser; ++i)
npara = npara + transfv.q[i] + transfv.p[i];
npara = npara + arimav.p + arimav.q + arimav.bigp + arimav.bigq + nseries;
if (npara >= 1) {
if (!(para = nAG_ALLOC(npara, double)) ||
!(sd = nAG_ALLOC(npara, double)) ||
!(xxy = nAG_ALLOC(nxxy * nseries, double)))
{
printf("Allocation failure\n");
exit_status = -1;
goto END;
}
tdxxy = nseries;
for (i = 0; i < npara; ++i)
scanf("%lf", ¶[i]);
for (i = 0; i < nxxy; ++i)
for (j = 0; j < nseries; ++j)
scanf("%lf", &XXY(i, j));
/* nag_tsa_multi_inp_model_estim (g13bec), see above. */
fflush(stdout);
nag_tsa_multi_inp_model_estim(&arimav, nseries, &transfv, para,
npara, nxxy, xxy, tdxxy, sd, &rss,
&objf, &df, &options, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_tsa_multi_inp_model_estim (g13bec)"
".\n%s\n", fail.message);
exit_status = 1;
goto END;
}
printf("\nThe correlation matrix is \n\n");
for (i = 0; i < npara; ++i)
for (j = 0; j < npara; ++j)
printf("%10.4f%c", CM(i, j), (j % 5 == 4) ? '\n' : ' ');
printf("\nThe residuals and the z and n values are\n\n");
printf(" i res[i] z(t) noise(t)\n\n");
for (i = 0; i < nxxy; ++i) {
if (i + 1 <= options.lenres) {
printf("%4ld%15.3f", i + 1, options.res[i]);
for (j = 0; j < nseries - 1; ++j)
printf("%15.3f ", ZT(i, j));
printf("%15.3f\n", options.noise[i]);
}
}
}
else {
printf("npara is out of range: npara = %-3ld\n", npara);
/* nag_tsa_free (g13xzc).
* Freeing function for use with g13 option setting
*/
nag_tsa_free(&options);
/* nag_tsa_trans_free (g13bzc), see above. */
nag_tsa_trans_free(&transfv);
exit_status = 1;
goto END;
}
}
else {
printf("One or both of nxxy and nseries are out of range:"
" nxxy = %-3ld while nseries = %-3ld\n",
nxxy, nseries);
exit_status = 1;
goto END;
}
/* nag_tsa_trans_free (g13bzc), see above. */
nag_tsa_trans_free(&transfv);
/* nag_tsa_free (g13xzc), see above. */
nag_tsa_free(&options);
END:
nAG_FREE(para);
nAG_FREE(sd);
nAG_FREE(xxy);
return exit_status;
}
