Keyword: 共役勾配, ランチョス, Lanczos, スパース, 対称, 線形連立方程式
概要
本サンプルは共役勾配／ランチョス（Lanczos）法を用いて実スパース対称線形連立方程式を解くC言語によるサンプルプログラムです。 本サンプルは共役勾配を用いて以下に示される対称線形連立方程式を解いて解を出力します。
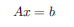
※本サンプルはnAG Cライブラリに含まれる関数 nag_sparse_sym_chol_sol() のExampleコードです。本サンプル及び関数の詳細情報は nag_sparse_sym_chol_sol のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
（本関数の詳細はnag_sparse_sym_chol_sol のマニュアルページを参照）1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
| このデータをダウンロード |
nag_sparse_sym_chol_sol (f11jcc) Example Program Data 7 n 16 nnz 1 0.0 lfill, dtol Nag_SparseSym_CG method Nag_SparseSym_UnModFact 0.0 mic dscale Nag_SparseSym_MarkPiv pstrat 1.0e-6 100 tol, maxitn 4. 1 1 1. 2 1 5. 2 2 2. 3 3 2. 4 2 3. 4 4 -1. 5 1 1. 5 4 4. 5 5 1. 6 2 -2. 6 5 3. 6 6 2. 7 1 -1. 7 2 -2. 7 3 5. 7 7 a[i-1], irow[i-1], icol[i-1], i=1,...,nnz 15. 18. -8. 21. 11. 10. 29. b[i-1], i=1,...,n 0. 0. 0. 0. 0. 0. 0. x[i-1], i=1,...,n
- １行目はタイトル行で読み飛ばされます。
- ２行目に行列Aの次数(n)を指定しています。
- ３行目に行列Aの下三角部分の非ゼロ要素の数(nnz)を指定しています。
- ４行目の１番目のパラメータ(lfill)は値が0以上の場合、分解で許されたフィル（fill）の最大レベルを指定しています。２番目のパラメータ(dtol)は、１番目のパラメータの値が負の値の場合、フィルイン（fill-in）を制御するためのドロップ許容値を指定しています。１番目のパラメータの値が0以上の場合は２番目のパラメータの値は参照されません。
- ５行目に反復手法(method)を指定しています。"Nag_SparseSym_CG"は共役勾配法（Conjugate Gradient method）を意味します。
- ６行目には行の合計を保持するためにコレスキー分解が修正されるかどうかを示すフラグ(mic)と対角スケーリング引数(dscale)を指定しています。 "Nag_SparseSym_UnModFact"はコレスキー分解が修正されないことを意味します。
- ７行目にピボット法(pstrat)を指定しています。"Nag_SparseSym_MarkPiv"はMarkowitz法を用いて対角ピボットが実行されることを意味します。
- ８行目に許容値(tol)と最大反復数(maxitn)を指定しています。
- ９～２４行目に行列Aの非ゼロ要素、行列Aの非ゼロ要素の行インデックス(irow)、列インデックス(icol)を指定しています。
- ２５～２６行目に右辺ベクトルBを指定しています。
- ２７～２８行目に解ベクトルxの初期近似値を指定しています。
出力結果
（本関数の詳細はnag_sparse_sym_chol_sol のマニュアルページを参照）1 2 3 4 5 6 7 8 9 10
| この出力例をダウンロード |
nag_sparse_sym_chol_sol (f11jcc) Example Program Results
Converged in 1 iterations
Final residual norm = 7.105e-15
1.0000e+00
2.0000e+00
3.0000e+00
4.0000e+00
5.0000e+00
6.0000e+00
7.0000e+00
- ２行目には１回の反復で収束したことが示されています。
- ３行目に最終的な残差ノルムが出力されています。
- ４～１０行目に解ベクトルxの改良された近似値が出力されています。
ソースコード
（本関数の詳細はnag_sparse_sym_chol_sol のマニュアルページを参照）
※本サンプルソースコードはnAG数値計算ライブラリ（Windows, Linux, MAC等に対応）の関数を呼び出します。
サンプルのコンパイル及び実行方法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143
| このソースコードをダウンロード |
/* nag_sparse_sym_chol_sol (f11jcc) Example Program.
*
* CLL6I261D/CLL6I261DL Version.
*
* Copyright 2017 Numerical Algorithms Group.
*
* Mark 26.1, 2017.
*
*/
#include <nag.h>
#include <stdio.h>
#include <nag_stdlib.h>
#include <nag_string.h>
#include <nagf11.h>
int main(void)
{
double dtol;
double *a = 0, *b = 0;
double *x = 0;
double rnorm, dscale;
double tol;
Integer exit_status = 0;
Integer *icol = 0;
Integer *ipiv = 0, nnzc, *irow = 0, *istr = 0;
Integer i;
Integer n;
Integer lfill, npivm;
Integer maxitn;
Integer itn;
Integer nnz;
Integer num;
char nag_enum_arg[40];
Nag_SparseSym_Method method;
Nag_SparseSym_Piv pstrat;
Nag_SparseSym_Fact mic;
Nag_Sparse_Comm comm;
NagError fail;
INIT_FAIL(fail);
printf("nag_sparse_sym_chol_sol (f11jcc) Example Program Results\n");
/* Skip heading in data file */
scanf(" %*[^\n]");
/* Read algorithmic parameters */
scanf("%ld%*[^\n]", &n);
scanf("%ld%*[^\n]", &nnz);
scanf("%ld%lf%*[^\n]", &lfill, &dtol);
scanf("%39s%*[^\n]", nag_enum_arg);
/* nag_enum_name_to_value (x04nac).
* Converts nAG enum member name to value
*/
method = (Nag_SparseSym_Method) nag_enum_name_to_value(nag_enum_arg);
scanf("%39s%lf%*[^\n]", nag_enum_arg, &dscale);
mic = (Nag_SparseSym_Fact) nag_enum_name_to_value(nag_enum_arg);
scanf("%39s%*[^\n]", nag_enum_arg);
pstrat = (Nag_SparseSym_Piv) nag_enum_name_to_value(nag_enum_arg);
scanf("%lf%ld%*[^\n]", &tol, &maxitn);
/* Read the matrix a */
/* Allocate memory */
num = 2 * nnz;
irow = nAG_ALLOC(num, Integer);
icol = nAG_ALLOC(num, Integer);
a = nAG_ALLOC(num, double);
b = nAG_ALLOC(n, double);
x = nAG_ALLOC(n, double);
istr = nAG_ALLOC(n + 1, Integer);
ipiv = nAG_ALLOC(num, Integer);
if (!irow || !icol || !a || !x || !istr || !ipiv) {
printf("Allocation failure\n");
return EXIT_FAILURE;
}
for (i = 1; i <= nnz; ++i)
scanf("%lf%ld%ld%*[^\n]", &a[i - 1], &irow[i - 1],
&icol[i - 1]);
/* Read right-hand side vector b and initial approximate solution x */
for (i = 1; i <= n; ++i)
scanf("%lf", &b[i - 1]);
scanf(" %*[^\n]");
for (i = 1; i <= n; ++i)
scanf("%lf", &x[i - 1]);
scanf("%*[^\n]");
/* Calculate incomplete Cholesky factorization */
/* nag_sparse_sym_chol_fac (f11jac).
* Incomplete Cholesky factorization (symmetric)
*/
nag_sparse_sym_chol_fac(n, nnz, &a, &num, &irow, &icol, lfill, dtol, mic,
dscale, pstrat, ipiv, istr, &nnzc, &npivm, &comm,
&fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_sparse_sym_chol_fac (f11jac).\n%s\n",
fail.message);
exit_status = 1;
goto END;
}
/* Solve Ax = b */
/* nag_sparse_sym_chol_sol (f11jcc).
* Solver with incomplete Cholesky preconditioning
* (symmetric)
*/
nag_sparse_sym_chol_sol(method, n, nnz, a, num, irow, icol, ipiv, istr, b,
tol, maxitn, x, &rnorm, &itn, &comm, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_sparse_sym_chol_sol (f11jcc).\n%s\n",
fail.message);
exit_status = 1;
goto END;
}
printf(" %s%10ld%s\n", "Converged in", itn, " iterations");
printf(" %s%16.3e\n", "Final residual norm =", rnorm);
/* Output x */
for (i = 1; i <= n; ++i)
printf(" %16.4e\n", x[i - 1]);
END:
nAG_FREE(irow);
nAG_FREE(icol);
nAG_FREE(a);
nAG_FREE(b);
nAG_FREE(x);
nAG_FREE(ipiv);
nAG_FREE(istr);
return exit_status;
}