Keyword: ロバスト回帰, M推定量
概要
本サンプルはロバスト回帰のM推定量の計算を行うC言語によるサンプルプログラムです。 本サンプルは以下に示されるデータについてロバスト回帰のM推定量の計算を行います。
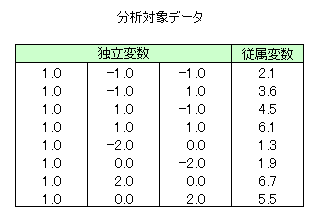
※本サンプルはnAG Cライブラリに含まれる関数 nag_robust_m_regsn_estim() のExampleコードです。本サンプル及び関数の詳細情報は nag_robust_m_regsn_estim のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本関数の詳細はnag_robust_m_regsn_estim のマニュアルページを参照)| このデータをダウンロード |
nag_robust_m_regsn_estim (g02hac) Example Program Data 8 3 1. -1. -1. 2.1 1. -1. 1. 3.6 1. 1. -1. 4.5 1. 1. 1. 6.1 1. -2. 0. 1.3 1. 0. -2. 1.9 1. 2. 0. 6.7 1. 0. 2. 5.5 Nag_SchweppeReg Nag_HampelFun Nag_SigmaChi Nag_CovMatObs 3.0 1.5 3.0 4.5 1.5
- 1行目はタイトル行で読み飛ばされます。
- 2行目は観測値の数(n)と独立変数の数(m)を指定しています。
- 3〜10行目に独立変数の観測値(x)と従属変数の観測値(y)を指定しています。
- 11行目の1番目のパラメータ(regtype)は実行される回帰の種類を指定しています。 "Nag_SchweppeReg"はSchweppeタイプの回帰を意味します。2番めのパラメータ(psifun)はどのΨ関数が使用されるかを指定しています。 "Nag_HampelFun"はHampelの区分線形関数が使用されることを意味します。3番目のパラメータ(sigma_est)はσの推定方法を指定しています。 "Nag_SigmaChi"はσがχ関数を使用して推定されることを意味します。
- 12行目の1番目のパラメータは共分散行列の推定で使用される近似法(covmat_est)を指定しています。"Nag_CovMatObs"は期待値を観測値で置き換えることを意味します。 2番目のパラメータ(cucv)はKrasker-Welschの重みのu関数の定数を指定しています。
- 13行目はHampelの区分線形関数のパラメータ(hpsi)を指定しています。
- 14行目はχ関数の定数(dchi)を指定しています。
出力結果
(本関数の詳細はnag_robust_m_regsn_estim のマニュアルページを参照)| この出力例をダウンロード |
nag_robust_m_regsn_estim (g02hac) Example Program Results
** Iteration monitoring for weights **
Iteration 1 max(abs(s(i,j))) = 1.93661e-01
A
Row
1 1.04e+00
2 0.00e+00 8.05e-01
3 0.00e+00 0.00e+00 8.05e-01
Iteration 2 max(abs(s(i,j))) = 9.25129e-02
A
Row
1 1.08e+00
2 0.00e+00 8.80e-01
3 0.00e+00 0.00e+00 8.80e-01
Iteration 3 max(abs(s(i,j))) = 3.56059e-02
A
Row
1 1.10e+00
2 0.00e+00 9.11e-01
3 0.00e+00 0.00e+00 9.11e-01
Iteration 4 max(abs(s(i,j))) = 1.29404e-02
A
Row
1 1.11e+00
2 0.00e+00 9.23e-01
3 0.00e+00 0.00e+00 9.23e-01
Iteration 5 max(abs(s(i,j))) = 4.81557e-03
A
Row
1 1.12e+00
2 0.00e+00 9.27e-01
3 0.00e+00 0.00e+00 9.27e-01
Iteration 6 max(abs(s(i,j))) = 1.81167e-03
A
Row
1 1.12e+00
2 0.00e+00 9.29e-01
3 0.00e+00 0.00e+00 9.29e-01
Iteration 7 max(abs(s(i,j))) = 6.81356e-04
A
Row
1 1.12e+00
2 0.00e+00 9.29e-01
3 0.00e+00 0.00e+00 9.29e-01
Iteration 8 max(abs(s(i,j))) = 2.56005e-04
A
Row
1 1.12e+00
2 0.00e+00 9.30e-01
3 0.00e+00 0.00e+00 9.30e-01
Iteration 9 max(abs(s(i,j))) = 9.61466e-05
A
Row
1 1.12e+00
2 0.00e+00 9.30e-01
3 0.00e+00 0.00e+00 9.30e-01
Iteration 10 max(abs(s(i,j))) = 3.61034e-05
A
Row
1 1.12e+00
2 0.00e+00 9.30e-01
3 0.00e+00 0.00e+00 9.30e-01
** Iteration monitoring for theta **
iteration sigma j theta rs
1 1.63136e+00 1 3.93035e+00 -3.93035e+00
2 1.24942e+00 -1.24942e+00
3 9.19080e-01 -9.19080e-01
2 4.48276e-01 1 3.96250e+00 -3.21549e-02
2 1.30833e+00 -5.89084e-02
3 8.58333e-01 6.07465e-02
3 3.70260e-01 1 3.97530e+00 -1.28013e-02
2 1.30833e+00 -4.44089e-16
3 8.41265e-01 1.70684e-02
4 3.23188e-01 1 3.98577e+00 -1.04731e-02
2 1.30833e+00 -2.22045e-16
3 8.27301e-01 1.39642e-02
5 2.91377e-01 1 3.99829e+00 -1.25129e-02
2 1.30833e+00 2.22045e-16
3 8.10617e-01 1.66839e-02
6 2.62746e-01 1 4.02376e+00 -2.54714e-02
2 1.30833e+00 2.22045e-16
3 7.76655e-01 3.39618e-02
7 2.26353e-01 1 4.04231e+00 -1.85490e-02
2 1.30833e+00 -4.44089e-16
3 7.51923e-01 2.47320e-02
8 2.09006e-01 1 4.04231e+00 0.00000e+00
2 1.30833e+00 0.00000e+00
3 7.51923e-01 0.00000e+00
9 2.04291e-01 1 4.04231e+00 0.00000e+00
2 1.30833e+00 0.00000e+00
3 7.51923e-01 0.00000e+00
10 2.03057e-01 1 4.04231e+00 0.00000e+00
2 1.30833e+00 0.00000e+00
3 7.51923e-01 0.00000e+00
11 2.02737e-01 1 4.04231e+00 0.00000e+00
2 1.30833e+00 0.00000e+00
3 7.51923e-01 0.00000e+00
12 2.02654e-01 1 4.04231e+00 0.00000e+00
2 1.30833e+00 0.00000e+00
3 7.51923e-01 0.00000e+00
13 2.02633e-01 1 4.04231e+00 0.00000e+00
2 1.30833e+00 0.00000e+00
3 7.51923e-01 0.00000e+00
14 2.02627e-01 1 4.04231e+00 0.00000e+00
2 1.30833e+00 0.00000e+00
3 7.51923e-01 0.00000e+00
Sigma = 0.2026
Theta Standard errors
4.0423 0.0384
1.3083 0.0272
0.7519 0.0311
Weights Residuals
0.5783 0.1179
0.5783 0.1141
0.5783 -0.0987
0.5783 -0.0026
0.4603 -0.1256
0.4603 -0.6385
0.4603 0.0410
0.4603 -0.0462
- 5行目に1回目の反復におけるSij(マニュアルページのセクション3を参照)の最大値が出力されています。
- 6〜10行目に行列Aの予測値が出力されています。
- 11〜16行目に2回目の反復の計算結果が出力されています。
- 17〜22行目に3回目の反復の計算結果が出力されています。
- 23〜28行目に4回目の反復の計算結果が出力されています。
- 29〜34行目に5回目の反復の計算結果が出力されています。
- 35〜40行目に6回目の反復の計算結果が出力されています。
- 41〜46行目に7回目の反復の計算結果が出力されています。
- 47〜52行目に8回目の反復の計算結果が出力されています。
- 53〜58行目に9回目の反復の計算結果が出力されています。
- 59〜64行目に10回目の反復の計算が出力されています。
- 69〜71行目に1回目の反復の σ の値、θのM推定量、θの最終値で求められるモデルからの残差が出力されています。
- 72〜74行目に2回目の反復の計算結果が出力されています。
- 75〜77行目に3回目の反復の計算結果が出力されています。
- 78〜80行目に4回目の反復の計算結果が出力されています。
- 81〜83行目に5回目の反復の計算結果が出力されています。
- 84〜86行目に6回目の反復の計算結果が出力されています。
- 87〜89行目に7回目の反復の計算結果が出力されています。
- 90〜92行目に8回目の反復の計算結果が出力されています。
- 93〜95行目に9回目の反復の計算結果が出力されています。
- 96〜98行目に10回目の反復の計算結果が出力されています。
- 99〜101行目に11回目の反復の計算結果が出力されています。
- 102〜104行目に12回目の反復の計算結果が出力されています。
- 105〜107行目に13回目の反復の計算結果が出力されています。
- 108〜110行目に14回目の反復の計算結果が出力されています。
- 111行目に σ の最終推定値が出力されています。
- 113〜117行目にθと標準誤差が出力されています。
- 119〜128行目に各観測値の重みと残差が出力されています。
ソースコード
(本関数の詳細はnag_robust_m_regsn_estim のマニュアルページを参照)
※本サンプルソースコードはnAG数値計算ライブラリ(Windows, Linux, MAC等に対応)の関数を呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
/* nag_robust_m_regsn_estim (g02hac) Example Program.
*
* CLL6I261D/CLL6I261DL Version.
*
* Copyright 2017 Numerical Algorithms Group.
*
* Mark 26.1, 2017.
*
*/
#include <nag.h>
#include <stdio.h>
#include <nag_stdlib.h>
#include <ctype.h>
#include <nagg02.h>
#define C(I, J) c[(I) *tdc + J]
#define X(I, J) x[(I) *tdx + J]
int main(void)
{
Integer exit_status = 0, i, j, m, max_iter, n, print_iter, tdc, tdx;
double *c = 0, cpsi, cucv, dchi, *hpsi = 0, *info = 0, *rs = 0,
sigma, *theta = 0;
double tol, *wt = 0, *x = 0, *y = 0;
char nag_enum_arg[40];
Nag_CovMatrixEst covmat_est;
Nag_PsiFun psifun;
Nag_RegType regtype;
Nag_SigmaEst sigma_est;
NagError fail;
INIT_FAIL(fail);
printf("nag_robust_m_regsn_estim (g02hac) Example Program Results\n\n");
/* Skip heading in data file */
scanf("%*[^\n]");
scanf("%ld %ld", &n, &m);
if (n > 1 && (m >= 1 && m <= n)) {
if (!(c = nAG_ALLOC(m * m, double)) ||
!(theta = nAG_ALLOC(m, double)) ||
!(x = nAG_ALLOC(n * m, double)) ||
!(y = nAG_ALLOC(n, double)) ||
!(rs = nAG_ALLOC(n, double)) ||
!(wt = nAG_ALLOC(n, double)) ||
!(info = nAG_ALLOC(4, double)) || !(hpsi = nAG_ALLOC(3, double)))
{
printf("Allocation failure\n");
exit_status = -1;
goto END;
}
tdc = m;
tdx = m;
}
else {
printf("Invalid n or m.\n");
exit_status = 1;
return exit_status;
}
/* Read in x and y */
for (i = 0; i < n; i++) {
for (j = 0; j < m; j++)
scanf("%lf", &X(i, j));
scanf("%lf", &y[i]);
}
/* Read in control parameters */
scanf(" %39s", nag_enum_arg);
/* nag_enum_name_to_value (x04nac).
* Converts nAG enum member name to value
*/
regtype = (Nag_RegType) nag_enum_name_to_value(nag_enum_arg);
scanf(" %39s", nag_enum_arg);
psifun = (Nag_PsiFun) nag_enum_name_to_value(nag_enum_arg);
scanf(" %39s", nag_enum_arg);
sigma_est = (Nag_SigmaEst) nag_enum_name_to_value(nag_enum_arg);
/* Read in appropriate weight function parameters. */
if (regtype != Nag_HuberReg) {
scanf(" %39s %lf", nag_enum_arg, &cucv);
covmat_est = (Nag_CovMatrixEst) nag_enum_name_to_value(nag_enum_arg);
}
if (psifun != Nag_Lsq) {
if (psifun == Nag_HuberFun)
scanf("%lf", &cpsi);
else
cpsi = 0.0;
if (psifun == Nag_HampelFun)
for (j = 0; j < 3; j++)
scanf("%lf", &hpsi[j]);
if (sigma_est == Nag_SigmaChi)
scanf("%lf", &dchi);
}
/* Set values of remaining parameters */
tol = 5e-5;
max_iter = 50;
/* Change print_iter to a positive value if monitoring information
* is required
*/
print_iter = 1;
sigma = 1.0e0;
for (i = 0; i < m; ++i)
theta[i] = 0.0e0;
/* nag_robust_m_regsn_estim (g02hac).
* Robust regression, standard M-estimates
*/
fflush(stdout);
nag_robust_m_regsn_estim(regtype, psifun, sigma_est, covmat_est, n, m, x,
tdx, y, cpsi, hpsi, cucv, dchi, theta, &sigma,
c, tdc, rs, wt, tol, max_iter, print_iter,
0, info, &fail);
if ((fail.code == NE_NOERROR) || (fail.code == NE_THETA_ITER_EXCEEDED) ||
(fail.code == NE_LSQ_FAIL_CONV) || (fail.code == NE_MAT_SINGULAR) ||
(fail.code == NE_WT_LSQ_NOT_FULL_RANK) ||
(fail.code == NE_REG_MAT_SINGULAR) ||
(fail.code == NE_COV_MAT_FACTOR_ZERO) ||
(fail.code == NE_VAR_THETA_LEQ_ZERO) ||
(fail.code == NE_ERR_DOF_LEQ_ZERO) ||
(fail.code == NE_ESTIM_SIGMA_ZERO)) {
if (fail.code != NE_NOERROR) {
printf("Error from nag_robust_m_regsn_estim (g02hac).\n%s\n",
fail.message);
printf(" Some of the following results may be unreliable\n");
}
printf("Sigma = %10.4f\n\n", sigma);
printf(" Theta Standard errors\n\n");
for (j = 0; j < m; ++j)
printf("%12.4f %13.4f\n", theta[j], C(j, j));
printf("\n Weights Residuals\n\n");
for (i = 0; i < n; ++i)
printf("%12.4f %13.4f\n", wt[i], rs[i]);
}
else {
printf("Error from nag_robust_m_regsn_estim (g02hac).\n%s\n",
fail.message);
exit_status = 1;
goto END;
}
END:
nAG_FREE(c);
nAG_FREE(theta);
nAG_FREE(x);
nAG_FREE(y);
nAG_FREE(rs);
nAG_FREE(wt);
nAG_FREE(info);
nAG_FREE(hpsi);
return exit_status;
}
