Keyword: 数値解析, ブラック・ショールズ, Black-Scholes
概要
本サンプルは数値解析によりブラック・ショールズ(Black-Scholes)方程式を解くC言語によるサンプルプログラムです。 本サンプルは行使価格50ドル、無リスク金利10%、ボラティリティ40%、無配当の5か月満期のアメリカンコールオプションについて以下に示されるブラック・ショールズ(Black-Scholes)方程式を解いてオプション価格とグリークス(Delta, Gamma, Lambda, Theta, Rho)を出力します。
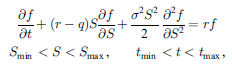
※本サンプルはnAG Cライブラリに含まれる関数 nag_pde_bs_1d_analytic() のExampleコードです。本サンプル及び関数の詳細情報は nag_pde_bs_1d_analytic のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本関数の詳細はnag_pde_bs_1d_analytic のマニュアルページを参照)| このデータをダウンロード |
nag_pde_bs_1d_analytic (d03ndc) Example Program Data 50. 0.4166667 0.1 0.0 0.4 21 4 0.0 100. 0.0 0.125
- 1行目はタイトル行で読み飛ばされます。
- 2行目に行使価格(x)を指定しています。
- 3行目にオプションの満期(tmat)を指定しています。
- 4行目に r の定値を指定しています。
- 5行目に q の定値を指定しています。
- 6行目に σ の定値(sigma)を指定しています。
- 7行目に株価の数(ns)と満期までの期間の数(nt)を指定しています。
- 8行目にオプション価格とグリークスが計算される株価の最小価格(smin)と最大価格(smax)を指定しています。
- 9行目にオプション価格とグリークスが計算される期間の最小値(tmin)と最大値(tmax)を指定しています。
出力結果
(本関数の詳細はnag_pde_bs_1d_analytic のマニュアルページを参照)| この出力例をダウンロード |
nag_pde_bs_1d_analytic (d03ndc) Example Program Results
Option Values
-------------
Stock Price | Time to Maturity (months)
| 5.0000e+00 4.5000e+00 4.0000e+00 3.5000e+00
--------------------------------------------------------------------------
0.0000e+00 | 0.0000e+00 0.0000e+00 0.0000e+00 0.0000e+00
5.0000e+00 | 4.4491e-19 4.5989e-21 1.5461e-23 1.0478e-26
1.0000e+01 | 5.5566e-10 5.5129e-11 3.1298e-12 8.0281e-14
1.5000e+01 | 4.7337e-06 1.2187e-06 2.2774e-07 2.7003e-08
2.0000e+01 | 7.2236e-04 3.1054e-04 1.1005e-04 2.9678e-05
2.5000e+01 | 1.6557e-02 9.6610e-03 5.0099e-03 2.2012e-03
3.0000e+01 | 1.3307e-01 9.4037e-02 6.1869e-02 3.6848e-02
3.5000e+01 | 5.6631e-01 4.5257e-01 3.4667e-01 2.5053e-01
4.0000e+01 | 1.6004e+00 1.3850e+00 1.1699e+00 9.5640e-01
4.5000e+01 | 3.4384e+00 3.1328e+00 2.8168e+00 2.4891e+00
5.0000e+01 | 6.1165e+00 5.7600e+00 5.3874e+00 4.9960e+00
5.5000e+01 | 9.5300e+00 9.1645e+00 8.7846e+00 8.3882e+00
6.0000e+01 | 1.3509e+01 1.3163e+01 1.2808e+01 1.2445e+01
6.5000e+01 | 1.7883e+01 1.7568e+01 1.7251e+01 1.6932e+01
7.0000e+01 | 2.2513e+01 2.2230e+01 2.1949e+01 2.1671e+01
7.5000e+01 | 2.7301e+01 2.7045e+01 2.6792e+01 2.6544e+01
8.0000e+01 | 3.2182e+01 3.1946e+01 3.1713e+01 3.1485e+01
8.5000e+01 | 3.7117e+01 3.6894e+01 3.6674e+01 3.6458e+01
9.0000e+01 | 4.2081e+01 4.1868e+01 4.1656e+01 4.1446e+01
9.5000e+01 | 4.7062e+01 4.6854e+01 4.6647e+01 4.6441e+01
1.0000e+02 | 5.2052e+01 5.1847e+01 5.1643e+01 5.1439e+01
Theta
-----
Stock Price | Time to Maturity (months)
| 5.0000e+00 4.5000e+00 4.0000e+00 3.5000e+00
--------------------------------------------------------------------------
0.0000e+00 | 0.0000e+00 0.0000e+00 0.0000e+00 0.0000e+00
5.0000e+00 | -4.4017e-17 -5.5977e-19 -2.3735e-21 -2.0936e-24
1.0000e+01 | -2.7827e-08 -3.3857e-09 -2.4163e-10 -8.0398e-12
1.5000e+01 | -1.3953e-04 -4.3864e-05 -1.0258e-05 -1.5706e-06
2.0000e+01 | -1.3287e-02 -6.9342e-03 -3.0567e-03 -1.0576e-03
2.5000e+01 | -1.9512e-01 -1.3714e-01 -8.7730e-02 -4.9018e-02
3.0000e+01 | -1.0161e+00 -8.5596e-01 -6.8695e-01 -5.1395e-01
3.5000e+01 | -2.8112e+00 -2.6426e+00 -2.4328e+00 -2.1723e+00
4.0000e+01 | -5.1662e+00 -5.1709e+00 -5.1500e+00 -5.0892e+00
4.5000e+01 | -7.2196e+00 -7.4540e+00 -7.7180e+00 -8.0183e+00
5.0000e+01 | -8.3848e+00 -8.7388e+00 -9.1543e+00 -9.6525e+00
5.5000e+01 | -8.6152e+00 -8.9372e+00 -9.3056e+00 -9.7329e+00
6.0000e+01 | -8.2058e+00 -8.4077e+00 -8.6186e+00 -8.8343e+00
6.5000e+01 | -7.5116e+00 -7.5845e+00 -7.6368e+00 -7.6553e+00
7.0000e+01 | -6.7905e+00 -6.7711e+00 -6.7202e+00 -6.6262e+00
7.5000e+01 | -6.1758e+00 -6.1099e+00 -6.0160e+00 -5.8893e+00
8.0000e+01 | -5.7084e+00 -5.6310e+00 -5.5359e+00 -5.4234e+00
8.5000e+01 | -5.3786e+00 -5.3103e+00 -5.2340e+00 -5.1533e+00
9.0000e+01 | -5.1582e+00 -5.1071e+00 -5.0551e+00 -5.0062e+00
9.5000e+01 | -5.0165e+00 -4.9835e+00 -4.9536e+00 -4.9298e+00
1.0000e+02 | -4.9281e+00 -4.9107e+00 -4.8979e+00 -4.8916e+00
Delta
-----
Stock Price | Time to Maturity (months)
| 5.0000e+00 4.5000e+00 4.0000e+00 3.5000e+00
--------------------------------------------------------------------------
0.0000e+00 | 0.0000e+00 0.0000e+00 0.0000e+00 0.0000e+00
5.0000e+00 | 3.1381e-18 3.5969e-20 1.3576e-22 1.0494e-25
1.0000e+01 | 1.4005e-09 1.5376e-10 9.7805e-12 2.8553e-13
1.5000e+01 | 6.1418e-06 1.7452e-06 3.6436e-07 4.9030e-08
2.0000e+01 | 5.6040e-04 2.6494e-04 1.0451e-04 3.1863e-05
2.5000e+01 | 8.3312e-03 5.3217e-03 3.0570e-03 1.5104e-03
3.0000e+01 | 4.5711e-02 3.5158e-02 2.5461e-02 1.6934e-02
3.5000e+01 | 1.3765e-01 1.1889e-01 9.9459e-02 7.9557e-02
4.0000e+01 | 2.8307e-01 2.6258e-01 2.3996e-01 2.1479e-01
4.5000e+01 | 4.5320e-01 4.3858e-01 4.2214e-01 4.0335e-01
5.0000e+01 | 6.1427e-01 6.0856e-01 6.0249e-01 5.9601e-01
5.5000e+01 | 7.4525e-01 7.4687e-01 7.4937e-01 7.5308e-01
6.0000e+01 | 8.4052e-01 8.4611e-01 8.5298e-01 8.6148e-01
6.5000e+01 | 9.0433e-01 9.1096e-01 9.1862e-01 9.2752e-01
7.0000e+01 | 9.4449e-01 9.5045e-01 9.5699e-01 9.6412e-01
7.5000e+01 | 9.6862e-01 9.7325e-01 9.7808e-01 9.8300e-01
8.0000e+01 | 9.8260e-01 9.8589e-01 9.8913e-01 9.9221e-01
8.5000e+01 | 9.9050e-01 9.9269e-01 9.9473e-01 9.9653e-01
9.0000e+01 | 9.9487e-01 9.9627e-01 9.9748e-01 9.9848e-01
9.5000e+01 | 9.9725e-01 9.9811e-01 9.9881e-01 9.9935e-01
1.0000e+02 | 9.9854e-01 9.9905e-01 9.9945e-01 9.9972e-01
Gamma
-----
Stock Price | Time to Maturity (months)
| 5.0000e+00 4.5000e+00 4.0000e+00 3.5000e+00
--------------------------------------------------------------------------
0.0000e+00 | 0.0000e+00 0.0000e+00 0.0000e+00 0.0000e+00
5.0000e+00 | 2.1246e-17 2.7112e-19 1.1536e-21 1.0211e-24
1.0000e+01 | 3.3102e-09 4.0468e-10 2.9020e-11 9.7029e-13
1.5000e+01 | 7.2660e-06 2.2982e-06 5.4080e-07 8.3319e-08
2.0000e+01 | 3.8245e-04 2.0111e-04 8.9333e-05 3.1153e-05
2.5000e+01 | 3.5190e-03 2.4960e-03 1.6118e-03 9.0924e-04
3.0000e+01 | 1.2392e-02 1.0554e-02 8.5660e-03 6.4838e-03
3.5000e+01 | 2.4348e-02 2.3181e-02 2.1626e-02 1.9580e-02
4.0000e+01 | 3.2765e-02 3.3274e-02 3.3650e-02 3.3795e-02
4.5000e+01 | 3.4099e-02 3.5763e-02 3.7655e-02 3.9828e-02
5.0000e+01 | 2.9625e-02 3.1360e-02 3.3403e-02 3.5860e-02
5.5000e+01 | 2.2600e-02 2.3743e-02 2.5052e-02 2.6569e-02
6.0000e+01 | 1.5672e-02 1.6137e-02 1.6603e-02 1.7048e-02
6.5000e+01 | 1.0123e-02 1.0119e-02 1.0032e-02 9.8216e-03
7.0000e+01 | 6.1999e-03 5.9720e-03 5.6534e-03 5.2154e-03
7.5000e+01 | 3.6474e-03 3.3666e-03 3.0215e-03 2.6027e-03
8.0000e+01 | 2.0815e-03 1.8329e-03 1.5510e-03 1.2387e-03
8.5000e+01 | 1.1610e-03 9.7196e-04 7.7211e-04 5.6851e-04
9.0000e+01 | 6.3660e-04 5.0529e-04 3.7553e-04 2.5382e-04
9.5000e+01 | 3.4468e-04 2.5884e-04 1.7950e-04 1.1099e-04
1.0000e+02 | 1.8494e-04 1.3118e-04 8.4708e-05 4.7786e-05
Lambda
------
Stock Price | Time to Maturity (months)
| 5.0000e+00 4.5000e+00 4.0000e+00 3.5000e+00
--------------------------------------------------------------------------
0.0000e+00 | 0.0000e+00 0.0000e+00 0.0000e+00 0.0000e+00
5.0000e+00 | 8.8525e-17 1.0167e-18 3.8453e-21 2.9781e-24
1.0000e+01 | 5.5171e-08 6.0702e-09 3.8694e-10 1.1320e-11
1.5000e+01 | 2.7247e-04 7.7565e-05 1.6224e-05 2.1871e-06
2.0000e+01 | 2.5496e-02 1.2066e-02 4.7644e-03 1.4538e-03
2.5000e+01 | 3.6656e-01 2.3400e-01 1.3431e-01 6.6299e-02
3.0000e+01 | 1.8588e+00 1.4248e+00 1.0279e+00 6.8080e-01
3.5000e+01 | 4.9710e+00 4.2595e+00 3.5323e+00 2.7983e+00
4.0000e+01 | 8.7374e+00 7.9857e+00 7.1787e+00 6.3084e+00
4.5000e+01 | 1.1508e+01 1.0863e+01 1.0167e+01 9.4094e+00
5.0000e+01 | 1.2344e+01 1.1760e+01 1.1134e+01 1.0459e+01
5.5000e+01 | 1.1394e+01 1.0773e+01 1.0104e+01 9.3768e+00
6.0000e+01 | 9.4033e+00 8.7137e+00 7.9693e+00 7.1602e+00
6.5000e+01 | 7.1285e+00 6.4127e+00 5.6514e+00 4.8412e+00
7.0000e+01 | 5.0632e+00 4.3894e+00 3.6936e+00 2.9815e+00
7.5000e+01 | 3.4194e+00 2.8406e+00 2.2661e+00 1.7080e+00
8.0000e+01 | 2.2203e+00 1.7596e+00 1.3235e+00 9.2488e-01
8.5000e+01 | 1.3981e+00 1.0534e+00 7.4380e-01 4.7920e-01
9.0000e+01 | 8.5941e-01 6.1393e-01 4.0558e-01 2.3986e-01
9.5000e+01 | 5.1846e-01 3.5040e-01 2.1600e-01 1.1686e-01
1.0000e+02 | 3.0824e-01 1.9677e-01 1.1294e-01 5.5750e-02
Rho
---
Stock Price | Time to Maturity (months)
| 5.0000e+00 4.5000e+00 4.0000e+00 3.5000e+00
--------------------------------------------------------------------------
0.0000e+00 | 0.0000e+00 0.0000e+00 0.0000e+00 0.0000e+00
5.0000e+00 | 6.3524e-18 6.5717e-20 2.2112e-22 1.4997e-25
1.0000e+01 | 5.6040e-09 5.5594e-10 3.1558e-11 8.0937e-13
1.5000e+01 | 3.6414e-05 9.3595e-06 1.7459e-06 2.0663e-07
2.0000e+01 | 4.3690e-03 1.8706e-03 6.6008e-04 1.7721e-04
2.5000e+01 | 7.9884e-02 4.6268e-02 2.3805e-02 1.0371e-02
3.0000e+01 | 5.1594e-01 3.6026e-01 2.3399e-01 1.3743e-01
3.5000e+01 | 1.7715e+00 1.3907e+00 1.0448e+00 7.3907e-01
4.0000e+01 | 4.0509e+00 3.4193e+00 2.8095e+00 2.2269e+00
4.5000e+01 | 7.0648e+00 6.2263e+00 5.3932e+00 4.5679e+00
5.0000e+01 | 1.0249e+01 9.2505e+00 8.2458e+00 7.2346e+00
5.5000e+01 | 1.3108e+01 1.1967e+01 1.0810e+01 9.6342e+00
6.0000e+01 | 1.5384e+01 1.4101e+01 1.2790e+01 1.1446e+01
6.5000e+01 | 1.7041e+01 1.5617e+01 1.4153e+01 1.2646e+01
7.0000e+01 | 1.8167e+01 1.6613e+01 1.5013e+01 1.3363e+01
7.5000e+01 | 1.8894e+01 1.7231e+01 1.5521e+01 1.3761e+01
8.0000e+01 | 1.9344e+01 1.7597e+01 1.5806e+01 1.3969e+01
8.5000e+01 | 1.9615e+01 1.7807e+01 1.5959e+01 1.4072e+01
9.0000e+01 | 1.9774e+01 1.7924e+01 1.6039e+01 1.4122e+01
9.5000e+01 | 1.9865e+01 1.7987e+01 1.6080e+01 1.4145e+01
1.0000e+02 | 1.9917e+01 1.8022e+01 1.6101e+01 1.4156e+01
- 6〜29行目には株価と満期までの期間に対応したオプションの値が出力されています。
- 33〜56行目には株価と満期までの期間に対応したThetaの値が出力されています。
- 60〜83行目には株価と満期までの期間に対応したDeltaの値が出力されています。
- 87〜110行目には株価と満期までの期間に対応したGammaの値が出力されています。
- 114〜137行目には株価と満期までの期間に対応したLambdaの値が出力されています。
- 141〜164行目には株価と満期までの期間に対応したRhoの値が出力されています。
ソースコード
(本関数の詳細はnag_pde_bs_1d_analytic のマニュアルページを参照)
※本サンプルソースコードはnAG数値計算ライブラリ(Windows, Linux, MAC等に対応)の関数を呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
/* nag_pde_bs_1d_analytic (d03ndc) Example Program.
*
* CLL6I261D/CLL6I261DL Version.
*
* Copyright 2017 Numerical Algorithms Group.
*
* Mark 26.1, 2017.
*/
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <nag.h>
#include <nag_stdlib.h>
#include <nagd03.h>
#define F(I, J) f[ns*((J) -1)+(I) -1]
#define THETA(I, J) theta[ns*((J) -1)+(I) -1]
#define DELTA(I, J) delta[ns*((J) -1)+(I) -1]
#define GAMMA(I, J) gamma[ns*((J) -1)+(I) -1]
#define LAMBDA(I, J) lambda[ns*((J) -1)+(I) -1]
#define RHO(I, J) rho[ns*((J) -1)+(I) -1]
int main(void)
{
double ds, dt, tmat, x;
Integer i, igreek, j, ns, nt, exit_status = 0;
double *delta = 0, *f = 0, *gamma = 0, *lambda = 0, q[3], r[3],
*rho = 0, *s = 0;
double sigma[3], *t = 0, *theta = 0, smin, smax, tmin, tmax;
Nag_Boolean gprnt[5] = { Nag_TRUE, Nag_TRUE, Nag_TRUE, Nag_TRUE, Nag_TRUE };
Nag_Boolean tdpar[3];
const char *gname[5] = { "Theta", "Delta", "Gamma", "Lambda", "Rho" };
NagError fail;
INIT_FAIL(fail);
printf("nag_pde_bs_1d_analytic (d03ndc) Example Program Results\n\n");
/* Skip heading in data file */
scanf("%*[^\n] ");
/* Read problem parameters */
scanf("%lf", &x);
scanf("%lf", &tmat);
scanf("%lf", &r[0]);
scanf("%lf", &q[0]);
scanf("%lf", &sigma[0]);
scanf("%ld%ld", &ns, &nt);
scanf("%lf%lf", &smin, &smax);
scanf("%lf%lf", &tmin, &tmax);
/* Allocate memory */
if (!(s = nAG_ALLOC(ns, double)) ||
!(t = nAG_ALLOC(nt, double)) ||
!(f = nAG_ALLOC(ns * nt, double)) ||
!(theta = nAG_ALLOC(ns * nt, double)) ||
!(delta = nAG_ALLOC(ns * nt, double)) ||
!(gamma = nAG_ALLOC(ns * nt, double)) ||
!(lambda = nAG_ALLOC(ns * nt, double)) ||
!(rho = nAG_ALLOC(ns * nt, double)))
{
printf("Allocation failure\n");
exit_status = 1;
goto END;
}
/* Set up input parameters for nag_pde_bs_1d (d03ncc) */
s[0] = smin;
s[ns - 1] = smax;
t[0] = tmin;
t[nt - 1] = tmax;
tdpar[0] = Nag_FALSE;
tdpar[1] = Nag_FALSE;
tdpar[2] = Nag_FALSE;
ds = (s[ns - 1] - s[0]) / (ns - 1.0);
dt = (t[nt - 1] - t[0]) / (nt - 1.0);
/* Loop over times */
for (j = 1; j <= nt; j++) {
t[j - 1] = t[0] + (j - 1) * dt;
/* Loop over stock prices */
for (i = 1; i <= ns; i++) {
s[i - 1] = s[0] + (i - 1) * ds;
/* Evaluate analytic solution of Black-Scholes equation */
/* nag_pde_bs_1d_analytic (d03ndc).
* Analytic solution of the Black-Scholes equations
*/
nag_pde_bs_1d_analytic(Nag_AmericanCall, x, s[i - 1], t[j - 1], tmat,
tdpar, r, q, sigma, &F(i, j), &THETA(i, j),
&DELTA(i, j), &GAMMA(i, j), &LAMBDA(i, j),
&RHO(i, j), &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_pde_bs_1d_analytic (d03ndc).\n%s\n",
fail.message);
exit_status = 1;
goto END;
}
}
}
/* Output option values */
printf("\n");
printf("Option Values\n");
printf("-------------\n");
printf("%14s | %s\n", "Stock Price", "Time to Maturity (months)");
printf("%14s | ", "");
for (i = 0; i < nt; i++)
printf(" %13.4e", 12.0 * (tmat - t[i]));
printf("\n");
for (i = 0; i < 74; i++)
printf("-");
printf("\n");
for (i = 1; i <= ns; i++) {
printf(" %13.4e | ", s[i - 1]);
for (j = 1; j <= nt; j++)
printf(" %13.4e", F(i, j));
printf("\n");
}
for (igreek = 0; igreek < 5; igreek++) {
if (!gprnt[igreek])
continue;
printf("\n");
printf("%s\n", gname[igreek]);
for (i = 0; i < (Integer) strlen(gname[igreek]); i++)
printf("-");
printf("\n");
printf("%14s | %s\n", "Stock Price", "Time to Maturity (months)");
printf("%14s | ", "");
for (i = 0; i < nt; i++)
printf(" %13.4e", 12.0 * (tmat - t[i]));
printf("\n");
for (i = 0; i < 74; i++)
printf("-");
printf("\n");
for (i = 1; i <= ns; i++) {
printf(" %13.4e | ", s[i - 1]);
switch (igreek) {
case 0:
for (j = 1; j <= nt; j++)
printf(" %13.4e", THETA(i, j));
break;
case 1:
for (j = 1; j <= nt; j++)
printf(" %13.4e", DELTA(i, j));
break;
case 2:
for (j = 1; j <= nt; j++)
printf(" %13.4e", GAMMA(i, j));
break;
case 3:
for (j = 1; j <= nt; j++)
printf(" %13.4e", LAMBDA(i, j));
break;
case 4:
for (j = 1; j <= nt; j++)
printf(" %13.4e", RHO(i, j));
break;
default:
break;
}
printf("\n");
}
}
END:
nAG_FREE(s);
nAG_FREE(t);
nAG_FREE(f);
nAG_FREE(theta);
nAG_FREE(delta);
nAG_FREE(gamma);
nAG_FREE(lambda);
nAG_FREE(rho);
return exit_status;
}
