Keyword: 偏相関, 分散共分散行列, 計算
概要
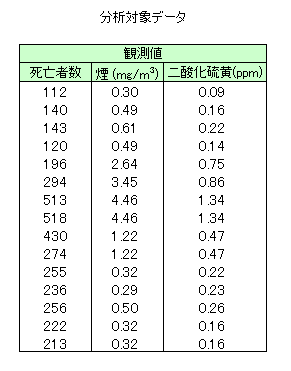
本サンプルは偏相関／分散共分散行列の計算を行うC言語によるサンプルプログラムです。 本サンプルは以下に示される観測値について相関・偏相関行列の計算を行います。
※本サンプルはnAG Cライブラリに含まれる関数 nag_partial_corr() のExampleコードです。本サンプル及び関数の詳細情報は nag_partial_corr のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
（本関数の詳細はnag_partial_corr のマニュアルページを参照）1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
| このデータをダウンロード |
nag_partial_corr (g02byc) Example Program Data 15 3 112 0.30 0.09 140 0.49 0.16 143 0.61 0.22 120 0.49 0.14 196 2.64 0.75 294 3.45 0.86 513 4.46 1.34 518 4.46 1.34 430 1.22 0.47 274 1.22 0.47 255 0.32 0.22 236 0.29 0.23 256 0.50 0.26 222 0.32 0.16 213 0.32 0.16 2 1 -1 -1 1
- １行目はタイトル行で読み飛ばされます。
- ２行目に観測値の数(n)と相関行列の変数の数(m)を指定しています。
- ３～１７行目に死亡者数と煙、二酸化硫黄の濃度を表す観測値(x)を指定しています。
- １９行目はY変数の数(ny)とX変数の数(nx)を指定しています。
- ２０行目はどの変数がX変数／Y変数に属するか(sz)を指定しています。0未満の値の場合はY変数、0より大きい値の場合はX変数に属することを意味します。
出力結果
（本関数の詳細はnag_partial_corr のマニュアルページを参照）1 2 3 4 5 6 7 8 9 10 11 12 13
| この出力例をダウンロード |
nag_partial_corr (g02byc) Example Program Results
Correlation Matrix
1.0000 0.7560 0.8309
1.0000 0.9876
1.0000
Partial Correlation Matrix
1.0000 -0.7381
1.0000
- ３～７行目に相関行列が出力されています。
- １０～１３行目に偏相関行列が出力されています。
ソースコード
（本関数の詳細はnag_partial_corr のマニュアルページを参照）
※本サンプルソースコードはnAG数値計算ライブラリ（Windows, Linux, MAC等に対応）の関数を呼び出します。
サンプルのコンパイル及び実行方法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110
| このソースコードをダウンロード |
/* nag_partial_corr (g02byc) Example Program.
*
* CLL6I261D/CLL6I261DL Version.
*
* Copyright 2017 Numerical Algorithms Group.
*
* Mark 26.1, 2017.
*/
#include <stdio.h>
#include <nag.h>
#include <nag_stdlib.h>
#include <nagg02.h>
#define X(I, J) x[((I) -1)*m + ((J) -1)]
#define R(I, J) r[((I) -1)*m + ((J) -1)]
int main(void)
{
Integer exit_status = 0, j, k, m, n, nx, ny, *sz = 0;
NagError fail;
double *r = 0, *std = 0, sw, *v = 0, *x = 0, *xbar = 0;
INIT_FAIL(fail);
printf("nag_partial_corr (g02byc) Example Program Results\n");
/* Skip heading in data file */
scanf("%*[^\n]");
scanf("%ld %ld", &n, &m);
if (!(r = nAG_ALLOC(m * m, double))
|| !(std = nAG_ALLOC(m, double))
|| !(v = nAG_ALLOC(m * m, double))
|| !(x = nAG_ALLOC(n * m, double))
|| !(xbar = nAG_ALLOC(m, double))
|| !(sz = nAG_ALLOC(m, Integer)))
{
printf("Allocation failure\n");
exit_status = -1;
goto END;
}
for (j = 1; j <= n; ++j)
for (k = 1; k <= m; ++k)
scanf("%lf", &X(j, k));
/* Calculate correlation matrix */
/* nag_corr_cov (g02bxc).
* Product-moment correlation, unweighted/weighted
* correlation and covariance matrix, allows variables to be
* disregarded
*/
nag_corr_cov(n, m, x, m, 0, 0, &sw, xbar, std, r, m, v, m, &fail);
if (fail.code == NE_NOERROR) {
/* Print the correlation matrix */
printf("\nCorrelation Matrix\n\n");
for (j = 1; j <= m; j++) {
for (k = 1; k <= m; k++)
if (j > k)
printf("%11s", "");
else
printf("%7.4f%4s", R(j, k), "");
printf("\n");
}
scanf("%ld %ld", &ny, &nx);
for (j = 1; j <= m; ++j)
scanf("%ld", &sz[j - 1]);
/* Calculate partial correlation matrix */
/* nag_partial_corr (g02byc).
* Computes partial correlation/variance-covariance matrix
* from correlation/variance-covariance matrix computed by
* nag_corr_cov (g02bxc)
*/
nag_partial_corr(m, ny, nx, sz, v, m, r, m, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_partial_corr (g02byc).\n%s\n", fail.message);
exit_status = 1;
goto END;
}
/* Print partial correlation matrix */
printf("\n");
printf("\nPartial Correlation Matrix\n\n");
for (j = 1; j <= ny; j++) {
for (k = 1; k <= ny; k++) {
if (j > k)
printf("%11s", "");
else if (j == k)
printf("%7.4f%4s", 1.0, "");
else
printf("%7.4f%4s", R(j, k), "");
}
printf("\n");
}
}
else {
printf("Error from nag_corr_cov (g02bxc).\n%s\n", fail.message);
exit_status = 1;
goto END;
}
END:
nAG_FREE(r);
nAG_FREE(std);
nAG_FREE(v);
nAG_FREE(x);
nAG_FREE(xbar);
nAG_FREE(sz);
return exit_status;
}