Keyword: 非線形最小二乗問題
概要
本サンプルは非線形最小二乗問題を解くC言語によるサンプルプログラムです。 本サンプルは以下に示される平方和を最小化する解を求めて、出力します。
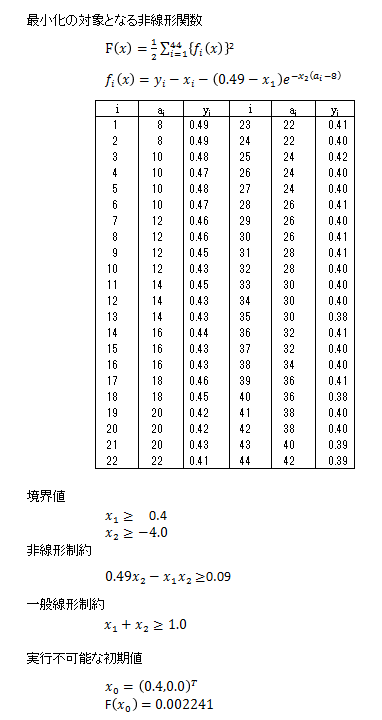
※本サンプルはnAG Cライブラリに含まれる関数 nag_opt_nlin_lsq() のExampleコードです。本サンプル及び関数の詳細情報は nag_opt_nlin_lsq のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本関数の詳細はnag_opt_nlin_lsq のマニュアルページを参照)| このデータをダウンロード |
nag_opt_nlin_lsq (e04unc) Example Program Data Values of m and n 44 2 Values of nclin and ncnln 1 1 Linear constraint matrix A 1.0 1.0 Objective vector y 0.49 0.49 0.48 0.47 0.48 0.47 0.46 0.46 0.45 0.43 0.45 0.43 0.43 0.44 0.43 0.43 0.46 0.45 0.42 0.42 0.43 0.41 0.41 0.40 0.42 0.40 0.40 0.41 0.40 0.41 0.41 0.40 0.40 0.40 0.38 0.41 0.40 0.40 0.41 0.38 0.40 0.40 0.39 0.39 Lower bounds 0.4 -4.0 1.0 0.0 Upper bounds 1.0e+25 1.0e+25 1.0e+25 1.0e+25 Initial estimate of x 0.4 0.0
- 1行目はタイトル行で読み飛ばされます。
- 4行目にF(x)に関連するサブ関数の数(m)、変数の数(n)を指定しています。
- 7行目には一般線形制約の数(nclin)、非線形制約の数(ncnln)を指定しています。
- 10行目には線形制約行列Aを指定しています。
- 13〜16行目には目的関数の定数ベクトルyの係数を指定しています。
- 19行目には変数の下限と線形制約、非線形制約の下限(bl)を指定しています。
- 22行目には変数の上限を線形制約、非線形制約の上限(bu)を指定しています。
- 25行目にはxの初期推定値を指定しています。
出力結果
(本関数の詳細はnag_opt_nlin_lsq のマニュアルページを参照)| この出力例をダウンロード |
nag_opt_nlin_lsq (e04unc) Example Program Results
Parameters to e04unc
--------------------
Number of variables........... 2
Linear constraints............ 1 Nonlinear constraints......... 1
start................... Nag_Cold
step_limit.............. 2.00e+00 machine precision....... 1.11e-16
lin_feas_tol............ 1.05e-08 nonlin_feas_tol......... 1.05e-08
optim_tol............... 3.26e-12 linesearch_tol.......... 9.00e-01
crash_tol............... 1.00e-02 f_prec.................. 4.37e-15
inf_bound............... 1.00e+20 inf_step................ 1.00e+20
max_iter................ 50 minor_max_iter.......... 50
hessian................. Nag_FALSE h_reset_freq............ 2
h_unit_init............. Nag_FALSE
f_diff_int.............. Automatic c_diff_int.............. Automatic
obj_deriv............... Nag_TRUE con_deriv............... Nag_TRUE
verify_grad....... Nag_SimpleCheck print_deriv............ Nag_D_Full
print_level......... Nag_Soln_Iter minor_print_level..... Nag_NoPrint
outfile................. stdout
Verification of the objective gradients.
----------------------------------------
All objective gradient elements have been set.
Simple Check:
The Jacobian seems to be ok.
The largest relative error was 1.04e-08 in subfunction 3
Verification of the constraint gradients.
-----------------------------------------
All constraint gradient elements have been set.
Simple Check:
The Jacobian seems to be ok.
The largest relative error was 1.89e-08 in constraint 1
Maj Mnr Step Merit function Violtn Norm Gz Cond Hz
0 2 0.0e+00 2.224070e-02 3.6e-02 8.5e-02 1.0e+00
1 1 1.0e+00 1.455402e-02 9.8e-03 1.5e-03 1.0e+00
2 1 1.0e+00 1.436491e-02 7.2e-04 4.9e-03 1.0e+00
3 1 1.0e+00 1.427013e-02 9.2e-06 2.9e-03 1.0e+00
4 1 1.0e+00 1.422989e-02 3.6e-05 1.6e-04 1.0e+00
5 1 1.0e+00 1.422983e-02 6.4e-08 5.4e-07 1.0e+00
6 1 1.0e+00 1.422983e-02 9.8e-13 3.4e-09 1.0e+00
Exit from NP problem after 6 major iterations, 8 minor iterations.
Varbl State Value Lower Bound Upper Bound Lagr Mult Residual
V 1 FR 4.19953e-01 4.00000e-01 None 0.0000e+00 1.9953e-02
V 2 FR 1.28485e+00 -4.00000e+00 None 0.0000e+00 5.2848e+00
L Con State Value Lower Bound Upper Bound Lagr Mult Residual
L 1 FR 1.70480e+00 1.00000e+00 None 0.0000e+00 7.0480e-01
N Con State Value Lower Bound Upper Bound Lagr Mult Residual
N 1 LL -9.76885e-13 0.00000e+00 None 3.3358e-02 -9.7689e-13
Optimal solution found.
Final objective value = 1.4229835e-02
- 3〜22行目に以下に示すプログラムのオプション引数が出力されています。
Number of variables 変数の数。 Linear constraints 線形制約の数。 Nonlinear constraints 非線形制約の数。 start 初期のワーキングセットがどのように選ばれるかを示しています。"Nag_Cold"は変数や制約の値に基づいて初期のワーキングセットが選ばれていることを意味します。 step_limit 直線探索(line search)の最初のステップでの変数の変化の最大値。 machine precision マシンの精度。 lin_feas_tol 実行可能点での線形制約の許容可能な絶対的違反の最大値。 nonlin_feas_tol 実行可能点での非線形制約の許容可能な絶対的違反の最大値。 optim_tol 最後の反復で解を近似させたい精度。 linesearch_tol 各反復で進むステップαが探索方向に沿ってメリット関数の最小値を近似する際の精度。 crash_tol 初期のワーキングセットに含まれる下限/上限や不等式制約が下限/上限のこの範囲内にあることを示しています。 f_prec 問題関数F(X)とc(x)が計算される際の精度の基準。 inf_bound 問題の制約の定義における無限境界。 inf_step 無限解へのステップと見なされる変数の変化の大きさ。 max_iter 大きな反復の最大数。 minor_max_iter 境界や線形制約に関して実行可能点を探索するための最大反復数。 hessian プログラムの引数hの内容を制御します。"Nag_FALSE"は引数hが変換され並べ替えられた行列HQのコレスキー因子を含むことを意味しています。 h_reset_freq この数の反復ごとに近似ヘッセ行列をJTJに戻します。 h_unit_init "Nag_FALSE"の場合、上三角行列Rの初期値がJTJに設定されます。"Nag_TRUE"の場合、Rの初期値はユニット行列になります。 f_diff_int 有限差分による導関数の推定に使用される区間。"Automatic"は自動的に計算されることを意味します。 c_diff_int アルゴリズムが中心差分に変更された場合に差分区間として使用されます。 "Automatic"は自動的に計算されることを意味します。 obj_deriv 目的関数のヤコビ行列の全要素が関数objfunで提供されているかどうかを示しています。 con_deriv 制約のヤコビ行列の全要素が関数confunで提供されているかどうかを示しています。 verify_grad ユーザ提供関数objfunとconfunで計算される勾配要素について実行される導関数チェックのレベル。 "Nag_SimpleCheck"は目的関数と制約の勾配両方の導関数の簡易チェックが行われることを意味します。 print_deriv 導関数チェックの結果を出力するかどうかを制御します。"Nag_D_Full"は導関数チェックの詳細が出力されることを意味します。 print_level 結果出力のレベル。"Nag_Soln_Iter"は最終解と各反復の結果を出力することを意味します。 minor_print_level 小さな反復で生じる結果の出力のレベル。"Nag_NoPrint"は何も出力されないことを意味します。 outfile 結果が出力されるファイル名。"stdout"は標準出力を意味します。 - 34行目に相対誤差が出力されています。
- 46〜55行目には以下が出力されています。
Maj 大きな反復の回数。 Mnr 実行可能解生成フェーズや最適化フェーズで必要とされる小さな反復の回数。 Step 探索方向に進んだステップ幅。 Merit Function ラグランジュメリット関数の値。 Violtn 制約違反の数。 Norm Gz 縮小勾配のユークリッド・ノルム。 Cond Hz ラグランジュの縮小ヘッセ行列の条件数の推定値。 - 56行目にはNP問題を解くのに6回の反復が行われたことが示されています。
- 59〜62行目には以下が出力されています。
Varbl 変数を示す"V"、インデックス。 State 変数の状態。FRは下限も上限もワーキングセットにはないことを意味します。 Value 最後の反復での変数の値。 Lower Bound 下限。 Upper Bound 上限。 Lagr Mult 関連する境界制約のラグランジュ乗数。 Residual 残差(変数の値と近いほうの下限/上限との差)。 - 64〜65行目には以下が出力されています。
L Con 線形制約を示す"L"、インデックス。 State 制約の状態。FRは下限も上限もワーキングセットにはないことを意味します。 Value 最後の反復での制約の値。 Lower Bound 下限。 Upper Bound 上限。 Lagr Mult 関連する境界制約のラグランジュ乗数。 Residual 残差(制約の値と近いほうの下限/上限との差)。 - 66〜69行目には以下が出力されています。
N Con 非線形制約を示す"N"、インデックス。 State 制約の状態。LLは下限であることを意味します。 Value 最後の反復での制約の値。 Lower Bound 下限。 Upper Bound 上限。 Lagr Mult 関連する境界制約のラグランジュ乗数。 Residual 残差(制約の値と近いほうの下限/上限との差)。 - 71行目にNPの最適解が見つかったことが示されています。
- 73行目にNPの最終的な目的関数値が出力されています。
ソースコード
(本関数の詳細はnag_opt_nlin_lsq のマニュアルページを参照)
※本サンプルソースコードはnAG数値計算ライブラリ(Windows, Linux, MAC等に対応)の関数を呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
/* nag_opt_nlin_lsq (e04unc) Example Program.
*
* CLL6I261D/CLL6I261DL Version.
*
* Copyright 2017 Numerical Algorithms Group.
*
* Mark 26.1, 2017.
*
*
*/
#include <nag.h>
#include <stdio.h>
#include <string.h>
#include <nag_stdlib.h>
#include <math.h>
#include <nage04.h>
#ifdef __cplusplus
extern "C"
{
#endif
static void nAG_CALL objfun(Integer m, Integer n, const double x[],
double f[], double fjac[], Integer tdfjac,
Nag_Comm *comm);
static void nAG_CALL confun(Integer n, Integer ncnlin,
const Integer needc[], const double x[],
double conf[], double cjac[], Nag_Comm *comm);
#ifdef __cplusplus
}
#endif
static void nAG_CALL objfun(Integer m, Integer n, const double x[],
double f[], double fjac[], Integer tdfjac,
Nag_Comm *comm)
{
#define FJAC(I, J) fjac[(I) *tdfjac + (J)]
/* Initialized data */
static double a[44] = { 8.0, 8.0, 10.0, 10.0, 10.0, 10.0, 12.0, 12.0, 12.0,
12.0, 14.0, 14.0, 14.0, 16.0, 16.0, 16.0, 18.0, 18.0,
20.0, 20.0, 20.0, 22.0, 22.0, 22.0, 24.0, 24.0, 24.0,
26.0, 26.0, 26.0, 28.0, 28.0, 30.0, 30.0, 30.0, 32.0,
32.0, 34.0, 36.0, 36.0, 38.0, 38.0, 40.0, 42.0
};
/* Local variables */
double temp;
Integer i;
double x0, x1, ai;
/* Function to evaluate the objective subfunctions
* and their 1st derivatives.
*/
x0 = x[0];
x1 = x[1];
for (i = 0; i < m; ++i) {
ai = a[i];
temp = exp(-x1 * (ai - 8.0));
/* Evaluate objective subfunction f(i+1) only if required */
if (comm->needf == i + 1 || comm->needf == 0)
f[i] = x0 + (.49 - x0) * temp;
if (comm->flag == 2) {
FJAC(i, 0) = 1.0 - temp;
FJAC(i, 1) = -(.49 - x0) * (ai - 8.0) * temp;
}
}
} /* objfun */
static void nAG_CALL confun(Integer n, Integer ncnlin, const Integer needc[],
const double x[], double conf[], double cjac[],
Nag_Comm *comm)
{
#define CJAC(I, J) cjac[(I) *n + (J)]
/* Function to evaluate the nonlinear constraints and its 1st derivatives. */
if (comm->first == Nag_TRUE) {
/* First call to confun. Set all Jacobian elements to zero.
* Note that this will only work when options.obj_deriv = TRUE
* (the default).
*/
CJAC(0, 0) = CJAC(0, 1) = 0.0;
}
if (needc[0] > 0) {
conf[0] = -0.09 - x[0] * x[1] + 0.49 * x[1];
if (comm->flag == 2) {
CJAC(0, 0) = -x[1];
CJAC(0, 1) = -x[0] + 0.49;
}
}
} /* confun */
#define A(I, J) a[(I) *tda + J]
int main(void)
{
Integer exit_status = 0, i, j, m, n, nbnd, nclin, ncnlin, tda, tdfjac;
Nag_E04_Opt options;
Nag_Comm comm;
double *a = 0, *bl = 0, *bu = 0, *f = 0, *fjac = 0, objf, *x = 0;
double *y = 0;
NagError fail;
INIT_FAIL(fail);
printf("nag_opt_nlin_lsq (e04unc) Example Program Results\n");
fflush(stdout);
scanf(" %*[^\n]"); /* Skip heading in data file */
/* Read problem dimensions */
scanf(" %*[^\n]");
scanf("%ld%ld%*[^\n]", &m, &n);
scanf(" %*[^\n]");
scanf("%ld%ld%*[^\n]", &nclin, &ncnlin);
if (m > 0 && n > 0 && nclin >= 0 && ncnlin >= 0) {
nbnd = n + nclin + ncnlin;
if (!(x = nAG_ALLOC(n, double)) ||
!(a = nAG_ALLOC(nclin * n, double)) ||
!(f = nAG_ALLOC(m, double)) ||
!(y = nAG_ALLOC(m, double)) ||
!(fjac = nAG_ALLOC(m * n, double)) ||
!(bl = nAG_ALLOC(nbnd, double)) || !(bu = nAG_ALLOC(nbnd, double)))
{
printf("Allocation failure\n");
exit_status = -1;
goto END;
}
tda = n;
tdfjac = n;
}
else {
printf("Invalid m or n nclin or ncnlin.\n");
exit_status = 1;
return exit_status;
}
/* Read a, y, bl, bu and x from data file */
if (nclin > 0) {
scanf(" %*[^\n]");
for (i = 0; i < nclin; ++i)
for (j = 0; j < n; ++j)
scanf("%lf", &A(i, j));
}
/* Read the y vector of the objective */
scanf(" %*[^\n]");
for (i = 0; i < m; ++i)
scanf("%lf", &y[i]);
/* Read lower bounds */
scanf(" %*[^\n]");
for (i = 0; i < n + nclin + ncnlin; ++i)
scanf("%lf", &bl[i]);
/* Read upper bounds */
scanf(" %*[^\n]");
for (i = 0; i < n + nclin + ncnlin; ++i)
scanf("%lf", &bu[i]);
/* Read the initial point x */
scanf(" %*[^\n]");
for (i = 0; i < n; ++i)
scanf("%lf", &x[i]);
/* Set an option */
/* nag_opt_init (e04xxc).
* Initialization function for option setting
*/
nag_opt_init(&options);
/* Solve the problem */
/* nag_opt_nlin_lsq (e04unc), see above. */
nag_opt_nlin_lsq(m, n, nclin, ncnlin, a, tda, bl, bu, y, objfun,
confun, x, &objf, f, fjac, tdfjac, &options, &comm, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_opt_nlin_lsq (e04unc).\n%s\n", fail.message);
exit_status = 1;
}
/* nag_opt_free (e04xzc).
* Memory freeing function for use with option setting
*/
nag_opt_free(&options, "all", &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_opt_free (e04xzc).\n%s\n", fail.message);
exit_status = 1;
goto END;
}
END:
nAG_FREE(x);
nAG_FREE(a);
nAG_FREE(f);
nAG_FREE(y);
nAG_FREE(fjac);
nAG_FREE(bl);
nAG_FREE(bu);
return exit_status;
}
