Keyword: 主成分分析, 多変量解析
概要
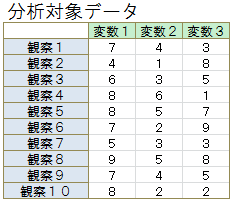
本サンプルは主成分分析を行うC言語によるサンプルプログラムです。 本サンプルは以下の「分析対象データ」に示される変数が３個で観察数が１０のデータを分析対象とします。 このサンプルでは主成分分析を行い、固有値、寄与度、χ二乗値、自由度、有意度、主成分負荷量、主成分スコアを出力します。
※本サンプルはnAG Cライブラリに含まれる関数 nag_mv_prin_comp() のExampleコードです。本サンプル及び関数の詳細情報は nag_mv_prin_comp のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
（本関数の詳細はnag_mv_prin_comp のマニュアルページを参照）1 2 3 4 5 6 7 8 9 10 11 12 13
| このデータをダウンロード |
nag_mv_prin_comp (g03aac) Example Program Data Nag_MatVarCovar Nag_ScoresEigenval Nag_FALSE 10 3 7.0 4.0 3.0 4.0 1.0 8.0 6.0 3.0 5.0 8.0 6.0 1.0 8.0 5.0 7.0 7.0 2.0 9.0 5.0 3.0 3.0 9.0 5.0 8.0 7.0 4.0 5.0 8.0 2.0 2.0 1 1 1 3 1 1 1 3
- １行目はタイトル行で読み飛ばされます。
- ２行目は計算の際に用いる行列の種類 (matrix=Nag_MatVarCovar)、計算に利用する主成分スコアのタイプ (scores=Nag_ScoresEigenval)、 重み付けをするかどうか (weight=Nag_FALSE)、観察数 (n=10)、変数の数 (m=3) を指定しています。
計算の際に用いる行列の種類に Nag_MatVarCovar が指定されていますが、これは分散共分散行列を用いることを意味します。
主成分スコアのタイプは計算で用いる主成分スコアの種類を指定しますが、ここで指定されているNag_ScoresEigenvalは主成分スコアに（分散が対応する固有値と同じになるように）標準化されたものを使う事が指定されています。
また各観察データに重みをつけることも可能ですが、ここではNag_FALSEを指定して重みを付けない事を指定しています。 - ５行目～１２行目は観察データ(x)を指定しています。各行はそれぞれの観察値であり、３つ（２行目で示される変数の数）の値を持っています。
- １３行目は計算で使う変数がどれであるかを示すパラメータ(isx)を指定しています。ここで 1 は計算で使う事を示しています。（0は計算で当該変数を使わないことを示します。ここで与える数字は変数の数分（ここでは3）なければなりません。 今回のデータはすべての変数を計算で使うので3つの 1 が与えられています。
最後の数字 (nvar=3) は出力として得たい主成分の数を指定しています。この数値は２行目で指定される変数の数を超えてはいけません。
出力結果
（本関数の詳細はnag_mv_prin_comp のマニュアルページを参照）1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
| この出力例をダウンロード |
nag_mv_prin_comp (g03aac) Example Program Results
Eigenvalues Percentage Cumulative Chisq DF Sig
variation variation
8.2739 0.6515 0.6515 8.6127 5.0000 0.1255
3.6761 0.2895 0.9410 4.1183 2.0000 0.1276
0.7499 0.0590 1.0000 0.0000 0.0000 0.0000
Principal component loadings
0.1376 0.6990 0.7017
0.2505 0.6609 -0.7075
-0.9583 0.2731 -0.0842
Principal component scores
1 2.151 -0.173 -0.107
2 -3.804 -2.887 -0.510
3 -0.153 -0.987 -0.269
4 4.707 1.302 -0.652
5 -1.294 2.279 -0.449
6 -4.099 0.144 0.803
7 1.626 -2.232 -0.803
8 -2.114 3.251 0.168
9 0.235 0.373 -0.275
10 2.746 -1.069 2.094
- １行目はタイトルです
- ３行目～８行目には各主成分の固有値 (Eigenvalues)、寄与度 (Percentage variation)、累積寄与度 (Cumulative variation)、χ二乗値 (Chisq)、自由度 (DF)、有意度 (Sig) がそれぞれ出力されます。６行目から８行目の各行は上から順番に第一主成分、第二主成分、第三主成分の各値を示しています。
- １０行目から１４行目に主成分負荷量を示しています。
- １６行目から２７行目は主成分スコアが出力されています。 行方向は観察データ、列方向は主成分をそれぞれ表しています。
ソースコード
（本関数の詳細はnag_mv_prin_comp のマニュアルページを参照）
※本サンプルソースコードはnAG数値計算ライブラリ（Windows, Linux, MAC等に対応）の関数を呼び出します。
サンプルのコンパイル及び実行方法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151
| このソースコードをダウンロード |
/* nag_mv_prin_comp (g03aac) Example Program.
*
* CLL6I261D/CLL6I261DL Version.
*
* Copyright 2017 Numerical Algorithms Group.
*
* Mark 26.1, 2017.
*
*/
#include <nag.h>
#include <stdio.h>
#include <nag_stdlib.h>
#include <nagg03.h>
#define X(I, J) x[(I) *tdx + J]
#define P(I, J) p[(I) *tdp + J]
#define E(I, J) e[(I) *tde + J]
#define V(I, J) v[(I) *tdv + J]
int main(void)
{
Integer exit_status = 0, i, *isx = 0, j, m, n, nvar, tde = 6, tdp, tdv, tdx;
Nag_PrinCompMat matrix;
Nag_PrinCompScores scores;
Nag_Boolean weight;
char nag_enum_arg[40];
double *e = 0, *p = 0, *s = 0, *v = 0, *wt = 0, *wtptr = 0;
double *x = 0;
NagError fail;
INIT_FAIL(fail);
printf("nag_mv_prin_comp (g03aac) Example Program Results\n\n");
/* Skip heading in data file */
scanf("%*[^\n]");
scanf("%39s", nag_enum_arg);
/* nag_enum_name_to_value (x04nac).
* Converts nAG enum member name to value
*/
matrix = (Nag_PrinCompMat) nag_enum_name_to_value(nag_enum_arg);
scanf("%39s", nag_enum_arg);
scores = (Nag_PrinCompScores) nag_enum_name_to_value(nag_enum_arg);
scanf("%39s", nag_enum_arg);
weight = (Nag_Boolean) nag_enum_name_to_value(nag_enum_arg);
scanf("%ld", &n);
scanf("%ld", &m);
if (n >= 2 && m >= 1) {
if (!(x = nAG_ALLOC((n) * (m), double)) ||
!(wt = nAG_ALLOC(n, double)) ||
!(s = nAG_ALLOC(m, double)) || !(isx = nAG_ALLOC(m, Integer)))
{
printf("Allocation failure\n");
exit_status = -1;
goto END;
}
tdx = m;
}
else {
printf("Invalid n or m.\n");
exit_status = 1;
return exit_status;
}
if (!weight) {
for (i = 0; i < n; ++i) {
for (j = 0; j < m; ++j)
scanf("%lf", &X(i, j));
}
}
else {
for (i = 0; i < n; ++i) {
for (j = 0; j < m; ++j)
scanf("%lf", &X(i, j));
scanf("%lf", &wt[i]);
}
wtptr = wt;
}
for (j = 0; j < m; ++j) {
scanf("%ld", &isx[j]);
}
scanf("%ld", &nvar);
if (nvar >= 1 && nvar <= MIN(n - 1, m)) {
if (!(p = nAG_ALLOC(nvar * nvar, double)) ||
!(e = nAG_ALLOC(nvar * 6, double)) ||
!(v = nAG_ALLOC(n * nvar, double)))
{
printf("Allocation failure\n");
exit_status = -1;
goto END;
}
tdp = nvar;
tde = 6;
tdv = nvar;
}
else {
printf("Invalid nvar.\n");
exit_status = 1;
goto END;
}
if (matrix == Nag_MatStandardised) {
for (j = 0; j < m; ++j)
scanf("%lf", &s[j]);
}
/* nag_mv_prin_comp (g03aac).
* Principal component analysis
*/
nag_mv_prin_comp(matrix, scores, n, m, x, tdx, isx, s, wtptr, nvar,
e, tde, p, tdp, v, tdv, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_mv_prin_comp (g03aac).\n%s\n", fail.message);
exit_status = 1;
goto END;
}
printf("Eigenvalues Percentage Cumulative Chisq DF Sig\n");
printf(" variation variation\n\n");
for (i = 0; i < nvar; ++i) {
for (j = 0; j < 6; ++j)
printf("%11.4f", E(i, j));
printf("\n");
}
printf("\nPrincipal component loadings \n\n");
for (i = 0; i < nvar; ++i) {
for (j = 0; j < nvar; ++j)
printf("%9.4f", P(i, j));
printf("\n");
}
printf("\nPrincipal component scores \n\n");
for (i = 0; i < n; ++i) {
printf("%2ld", i + 1);
for (j = 0; j < nvar; ++j)
printf("%9.3f", V(i, j));
printf("\n");
}
END:
nAG_FREE(x);
nAG_FREE(wt);
nAG_FREE(s);
nAG_FREE(isx);
nAG_FREE(p);
nAG_FREE(e);
nAG_FREE(v);
return exit_status;
}
リファレンス
サンプル入力データは Cooley W C and Lohnes P R (1971) Multivariate Data Analysis Wiley よりのデータです。