誤差解析
誤差解析(error
analysis)とは誤差の累積効果を分析しようとするものである。通常これらは丸め誤差(rounding
errors)、または打切り誤差(truncation
errors)である。例えば における多項式
における多項式 の値をホーナー法(Horner's
scheme, nested
multiplication)によって
の値をホーナー法(Horner's
scheme, nested
multiplication)によって のように評価する場合、係数
のように評価する場合、係数 と
と にどのような条件があれば妥当な解が得られるであろうか?この問いに答えるには誤差解析の実行が必要となる。
にどのような条件があれば妥当な解が得られるであろうか?この問いに答えるには誤差解析の実行が必要となる。
誤差解析は与えられた問題に対しアルゴリズムが安定であるか否かを確定する技術である。前進誤差解析(forward
error
analysis)は算出された解が厳密解にどれだけ近いかを議論する。後退誤差解析(backward
error
analysis)は算出された解が求解対象の問題に対しどれだけ満足の行くものかどうかを議論する。初めての場合、前進誤差解析ではなく後退誤差解析が関心の対象になるということに対し、驚かれるかも知れない。次の例は後退誤差と前進誤差の違いを例示したものである。
Example 4.14
(連立1次方程式)
今 とする。このとき
とする。このとき の厳密解は
の厳密解は で与えられる。ここで
で与えられる。ここで を方程式に対する近似解とし、残差(residual)ベクトル
を方程式に対する近似解とし、残差(residual)ベクトル を
を

|
(14) |
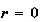 であるから、
であるから、 に近い解に対しては
に近い解に対しては が小さいものと期待することになる。今、近似解
が小さいものと期待することになる。今、近似解 について考えると
について考えると となることから、
となることから、 はかなり悪い解のように見える。しかしこのとき
はかなり悪い解のように見える。しかしこのとき となり、与えられた問題がほぼ解けたことになる。一方、近似解
となり、与えられた問題がほぼ解けたことになる。一方、近似解 について考えると
について考えると であるが
であるが となる。すなわち
となる。すなわち は
は に近いにもかかわらず、与えられた問題が解けたとは言いがたい。
に近いにもかかわらず、与えられた問題が解けたとは言いがたい。
連立1次方程式 の解が算出できたら(14)より簡単に残差が求められる。今、
の解が算出できたら(14)より簡単に残差が求められる。今、

|
(15) |
 が求まったとすると
が求まったとすると より、
より、 を厳密解に一致させるに必要な
を厳密解に一致させるに必要な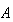 に対する摂動の尺度が得られたことになる。(15)
を満たす
に対する摂動の尺度が得られたことになる。(15)
を満たす は
は で与えられる。この式より
で与えられる。この式より 一方(15)より
一方(15)より
これより が導かれる。この特定の
が導かれる。この特定の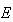 は
は を最小化する。
を最小化する。 であるから、それはフロベニアスノルム(Frobenius
norm)においても
であるから、それはフロベニアスノルム(Frobenius
norm)においても を最小化する。これは後退誤差(backward
error)に関する事後限界(posteriori
bound)を与える。
を最小化する。これは後退誤差(backward
error)に関する事後限界(posteriori
bound)を与える。
Example 4.15
(連立1次方程式の摂動)
Example
4.14の方程式 に対する数値解を
に対する数値解を とするとその残差は
とするとその残差は となる。このとき
となる。このとき
 である。
である。 であるから、この数値解は
であるから、この数値解は における小さな相対摂動に対応する。
における小さな相対摂動に対応する。
(6)より
従って がわかっていれば後退誤差の推定値より前進誤差(forward
error)の推定値を得ることができる。
がわかっていれば後退誤差の推定値より前進誤差(forward
error)の推定値を得ることができる。
一般的なルールとして概ね次が言える。
 |
後退誤差解析の概念は他の研究者によって導かれたものであるにせよ、真に理論と応用を開発し、(特に数値線形代数という側面において)誤差解析と安定性に対する理解をもたらしたのはJames Hardy Wilkinsonであった。古典的な書籍である Wilkinson [1963], Wilkinson [1965] を参照されたい。Wilkinsonの写真を図8に示す。Wilkinsonの伝統を受け継ぐ新しい書籍には Higham [2002] がある。今日における数値線形代数の確固たる基盤はWilkinsonの開拓者的業績に負うところが大きい。Wilkinson and Reinsch [1971] Note1 も参照。

図8 James Hardy Wilkinson
(1919-1986)
Wilkinsonは、誤差解析はうんざりさせられる、しかもしばしば細心の注意を要するものであるが、アルゴリズムの安定性を理解する上では本質的なものであると認めている。
| "アルゴリズムの安定性を決定付ける要因を明らかにすることによって、より良いアルゴリズムの開発が可能になった。固有ベクトルに関する逆反復法の適切な理解、及びFrancisによるQRアルゴリズムの開発は、この流れの研究における輝ける業績である。" "私にとって丸め誤差解析の主たる目的は洞察であった。" [Wilkinson, 1986, p. 197.] |
前進誤差と後退誤差に関する第2の例として、今度はExample 4.9の2次方程式について考えることにする。
Example 4.16
(2次方程式の誤差)
Example
4.9の2次方程式に対して標準的な計算式を使うと という2つの解が得られる。これに対して正しい解は
という2つの解が得られる。これに対して正しい解は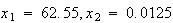 であるため、2番目の根は大きな前進誤差を有している。今、2次方程式を
であるため、2番目の根は大きな前進誤差を有している。今、2次方程式を という形で構成し、有効桁数を4桁で計算すると、
という形で構成し、有効桁数を4桁で計算すると、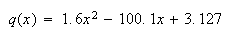 が得られる。定数項は元の値
が得られる。定数項は元の値 から大きく異なっているため、大きな後退誤差も見られる。従って標準的な手法は前向きにも後向きにも安定ではない。一方、計算結果である
から大きく異なっているため、大きな後退誤差も見られる。従って標準的な手法は前向きにも後向きにも安定ではない。一方、計算結果である に対しては
に対しては が得られるため、こちらは前向きにも後向きにも安定である。
が得られるため、こちらは前向きにも後向きにも安定である。
前向きには安定であるが後ろ向きには安定でない計算の例には多項式 の係数の計算がある。この場合、
の係数の計算がある。この場合、 はすべて同一の符合を持つため、
はすべて同一の符合を持つため、 の係数の計算において桁落ち(cancellation)は起らず、算出された係数値は厳密値に近いものとなる。従って前進誤差は小さいと言える。一方、Example
4.1が示すように、多項式の根は係数値のわずかな変化に敏感に反応し、その根は
の係数の計算において桁落ち(cancellation)は起らず、算出された係数値は厳密値に近いものとなる。従って前進誤差は小さいと言える。一方、Example
4.1が示すように、多項式の根は係数値のわずかな変化に敏感に反応し、その根は から大きくはずれることがある。
から大きくはずれることがある。
Example 4.17
(ill-conditionedな多項式)
根が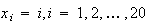 である多項式は
である多項式は で与えられる。今、
で与えられる。今、 の係数値が
の係数値が と計算されたとすると、
と計算されたとすると、 となる。従って係数値の計算における小さな誤差によって、厳密解から大きく異なる根を持った多項式が生み出されたことになる。この多項式についての議論については
Wilkinson [1963, Chapter 2, Section 9], Wilkinson [1984], Wilkinson [1985,
Section 2]
を参照されたい。
となる。従って係数値の計算における小さな誤差によって、厳密解から大きく異なる根を持った多項式が生み出されたことになる。この多項式についての議論については
Wilkinson [1963, Chapter 2, Section 9], Wilkinson [1984], Wilkinson [1985,
Section 2]
を参照されたい。
