カスタムアルゴリズム開発の事例

質量分析はサンプル物質の化学的構成を解析する際に用いられる方法です。細胞がサンプルの場合はその中の薬物や代謝産物の解析に用いられ、さらに３次元の人工的な固形物でも可能です。これらサンプルは光やイオンに照射されて、散乱されたイオンの飛行時間が検出器で測定されます。これによりイオンの質量電荷比が決定されます。

質量分析には様々な方法がありますが、最も重要なものは二次イオン質量分析法（SIMS）とマトリックス支援レーザー脱離イオン化法（MALDI）です。これらにおいてはデータはハイパースペクトルとして格納されます：各ピクセルにはデータの全スペクトルが保存され、これらは飛行時間チャネルへ分割され、そのカウント数が各チャネルに記録されます。

質量分析プロセス概念図	SIMS 装置

質量分析イメージングデータは巨大で複雑なものです。また雑音も存在し、特定のイメージング手法を用いるとアーチファクトが含まれる場合があります。こうした事柄が組み合わされて、このデータ解析と可視化を困難なものにしています。

これに加えて、イメージフュージョン法を用いれば更なる情報を得ることが出来ます。この方法は、複数の異なるスキャンデータを組み合わせて一つのイメージを作成します。下図の例においては、左図のイメージは低空間解像度でスキャンされており、その高解像度ケースが右図に示されています。しかしながら、各図の下に示してある通り、左図は明確な２つのピークを持つ高質量分析解像度を持ち、右図は低解像度になっています。イメージフュージョンの目的は、２つのイメージを組み合わせて高解像質量分析かつ高空間解像度を持つ一つのイメージを生成することです。

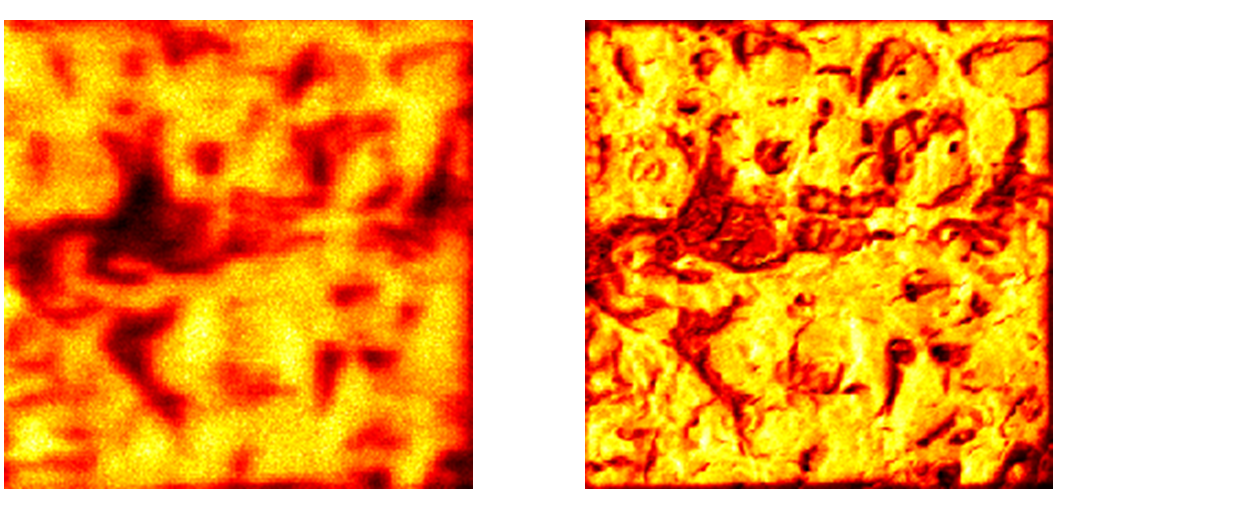
低空間解像および高空間解像度のサンプルスキャン
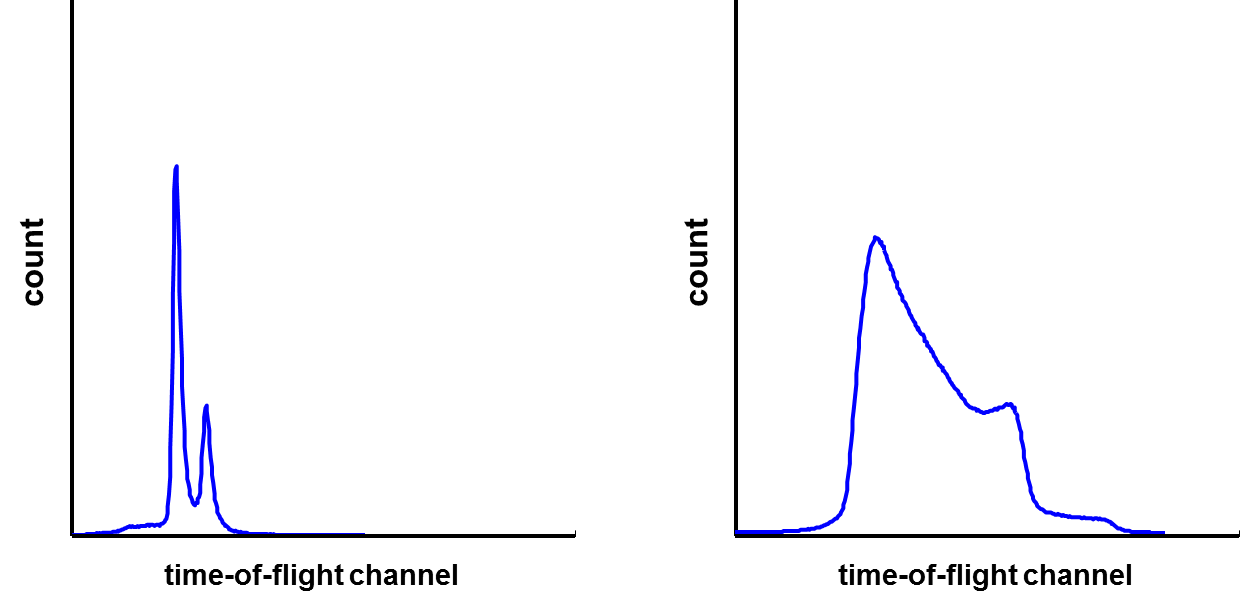
上の低／高空間解像度のサンプルスキャンに対応する飛行時間プロット：それぞれ高/低質量分析解像度を持つ

このようなイメージ統合ツールは、衛星画像のような他の分野で既に広く用いられていますが、そのソフトウェアや手法は微小光学解析分野においては有効性に欠ける場合があります。先述した雑音やアーチファクト、データサイズに関する問題が組み合わされて、質量分析におけるイメージフュージョンは計算量が膨大になります。

「nAG/NPL ハイパースペクトルイメージング・ライブラリ」は、高性能データ操作・解析ルーチン群で構成されたツールです。これらは、MALDI あるいは SIMS の raw データの読み込みからその処理まで、つまりイメージフュージョンの一貫したワークフローを可能にします。これらルーチン群は、マルチコアマシンを有効に活用するように並列化されています。

このライブラリーのインターフェイスはポリモルフィッククラスで構成され、MATLAB^® と C++ で利用可能であり、イメージマトリックスや様々な関数がカプセル化されています。ここでは MATLAB^® を用いたライブラリ利用の実例を示します。

raw データの読み込み

SIMS や MALDI 装置で生成された様々な出力 raw データをコンフィグレーションファイルに設定するところから始めます。ピーク選択のための "limits" ファイルやピクセルと飛行時間をグループ分けする"bin size"も指定することが出来ます。

  configs = '<path to>\input.config';

  % The input.config file points to the raw data and allows bins to be specified. Contents of input.config:
  %   coords = <path to>\raw.coords file
  %   limits = <path to>\limits.txt file #for use in peak selection later
  %   tofs = <path to>\raw.tofs file
  %   props = <path to>\properties.txt file
  %
  %   #Specify bin sizes, here we group 4x4 sets of pixels together and 16 time-of-flight channels:
  %   xbin = 4
  %   ybin = 4
  %   tofbin = 16

  img = SpecImageFactory(configs); 

オブジェクト img は、SpecImage クラスのインスタンスです。これは、ピクセル数×チャネル数のサイズのデータ行列を持ちます。データ行列の構築処理はマルチコア上で良好なスケール性を示します。

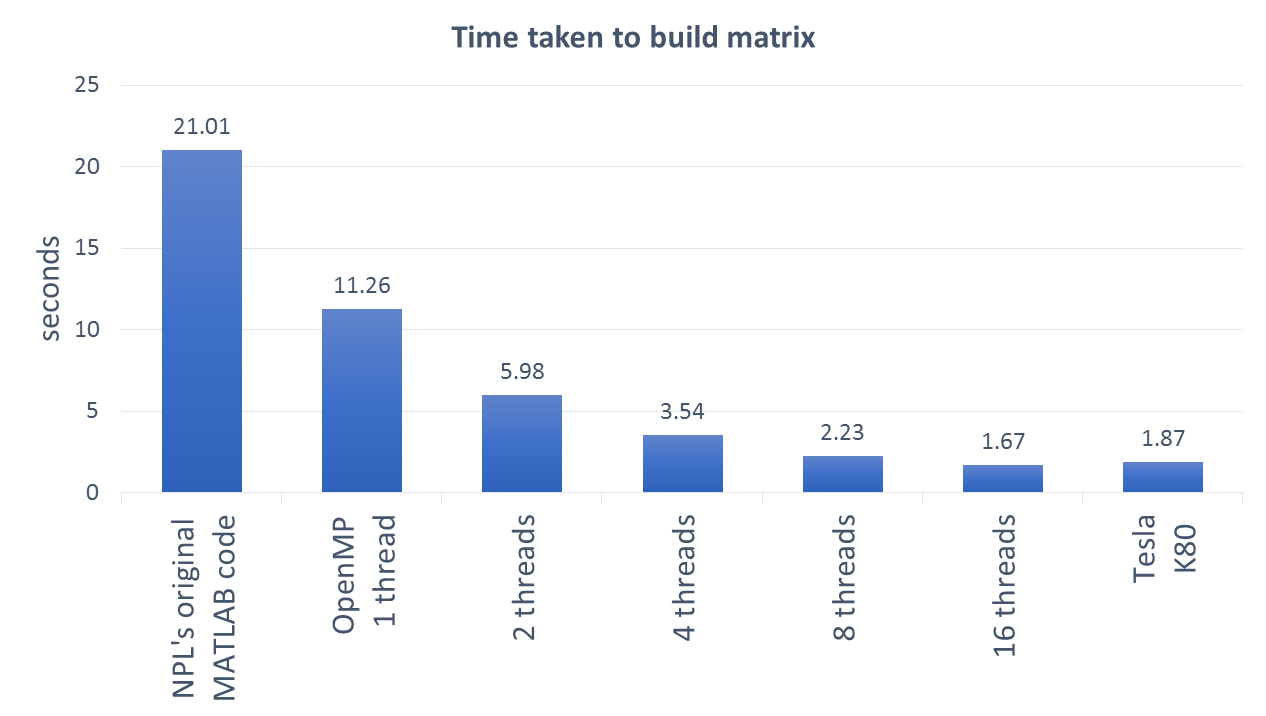
マルチコア CPU と K80 CPU 上でのデータ行列生成のスケール性。最左バーはオリジナルのNPLによるシリアル実行 MATLAB^® コードを示す。

SpecImage を照会すれば、以下の様にデータ行列に関する情報を取得できます。

  x = img.getXDim; % Number of pixels in the x direction
  y = img.getYDim; % Number of pixels in the y direction
  A = img.getMatrix; % Returns matrix in sparse format
  m = img.getNumPixels; % Number of pixels in the image matrix
  n = img.getNumChannels; % Number of channels in the image matrix: thus the data matrix is m x n

メモリーに格納された行列から直接 SpecImage を生成することも可能です。

プリプロセス関数

SpecImage クラスは２つのサブクラス、SIMSpecImage および MALDISpecImage を持ちます。これらはそれぞれ、SIMS と MALDI 装置に特定の機能がカプセル化されています。

データ解析の前に、その処理により適した形式へデータを変換する必要があります。この前処理は SISM か MALDI のどちらかを利用するかによって異なります。

SIMS イメージに対しては、Advanced dead-time correction とスケーリングを行います。Advanced dead-time correction（ADTC）は、SIMS 機器でデッドタイムウィンドウのデータを補正する変換です（デッドタイムウィンドウはデータ解析で偽のアーチファクトを導く可能性があります）。ADTC ステップに続いて、ADTC の非線形性を補正するために、データ行列に対角行列を前後に乗算してデータ行列をスケールします：

  img.advancedDeadTimeCorrection;
  img.scaleMatrix;

ADTCの詳細は文献：The accuracy and precision of the advanced Poisson dead-time correction and its importance for multivariate analysis of high mass resolution ToF-SIMS data, Bonnie J. Tyler, Surf. Interface Anal. 2014, 46, 581-590 を参照してください。

サブクラス SIMSpecImage および MALDISpecImage の両方で、ピーク選択が可能です。以前に img を構築した際に、コンフィグレーションファイルにピーク選択制約（limits）を定義しました。この制約を使用して飛行時間チャネルの数を減らし、データ行列サイズを小さくすることができます。ピークが重複している場合、特にビニング後に警告を受け取ることも可能です：

  img.peakSelect();

  **Warning:
  	 155 pairs of overlapping peak selection bins have been separated

解析の関数

SpecImage クラスの一部として様々なデータ解析関数が可能です。これらの関数を使用すると、データの次元を縮小したり、データの重要な側面を抽出したり、さまざまな方法でデータを分解したりすることができます。ここでは、データ行列のサイズは m × n、m はピクセル数、n は飛行時間チャネル数であると仮定します。

連続ウェーブレット変換

データ行列内の与えられたピクセル（行）に対して、様々な飛行時間チャネルのカウントをプロットすることができます：

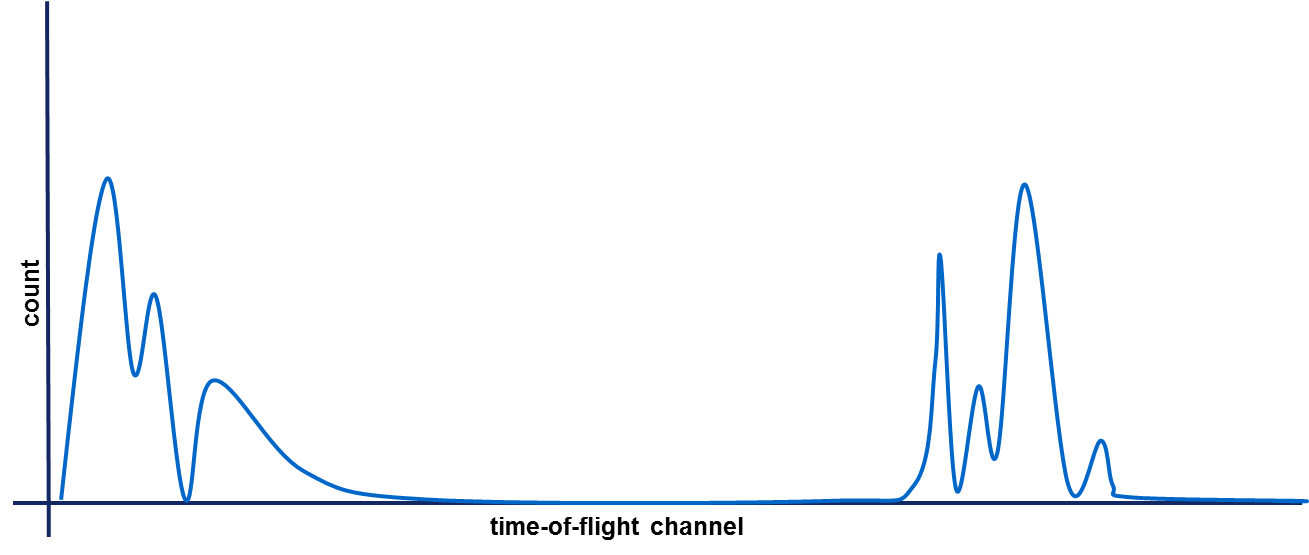
与えられたピクセルに関する飛行時間チャネルのカウント例

連続ウェーブレット変換では、マザーウェーブレット ψ のスケールかつ伸張されたバージョンで畳み込むことによって、以下の式の f$x$ で示されるこの曲線は分解されます：

$$\begin{eqnarray} C_{s,k}=\int_{-\infty}^{\infty} f(x) \frac{1}{\sqrt{s}} \overline{ψ} \left( \frac{x-k}{s} \right) dx \end{eqnarray}$$

マザーウェーブレットψは通常、下図のメキシカンハットあるいはハールウェーブレットと言ったコンパクトな台を持つ単純な関数です：

Mexican Hat wavelet	Haar wavelet

グラフ的には、以下に見るように、ウェーブレットの選択されたスケール s に対して繰り返し変換して信号 f$x$ とマッチさせます：

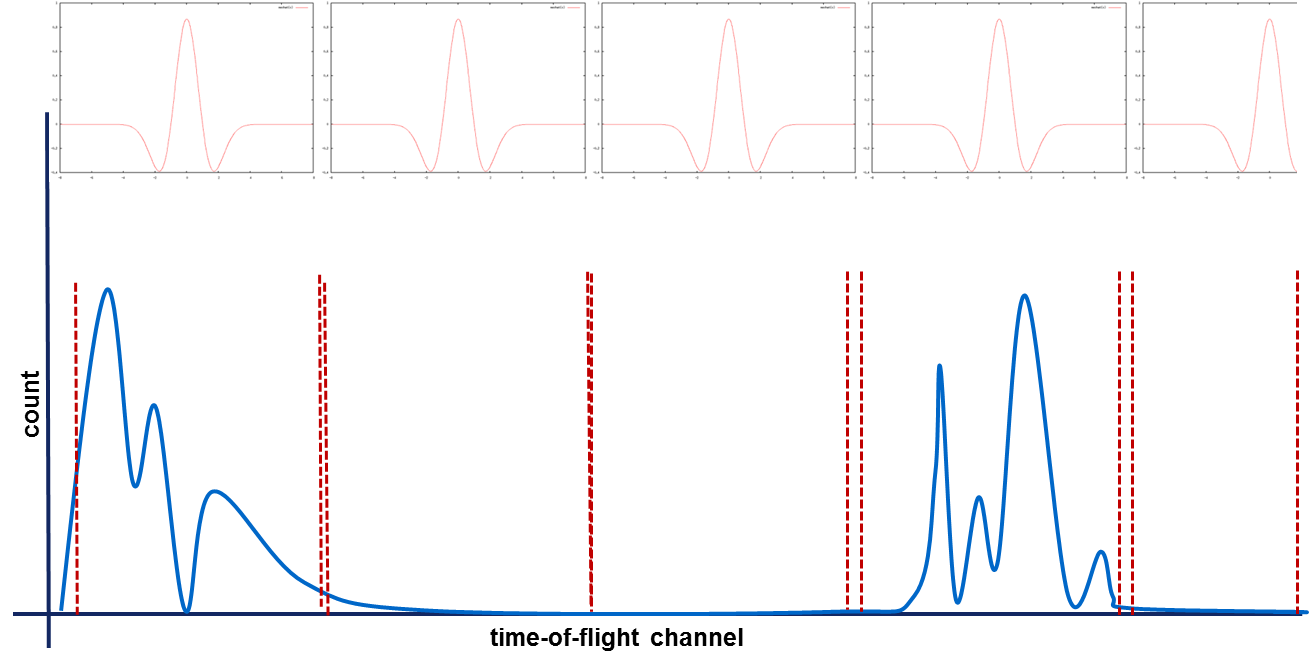
連続ウェーブレット変換

以下の例では、最初に解析で用いるスケールとピクセルを設定しています。ここでは、20 ピクセルと４つのバイナリースケールを選択し、zero end extension（これは領域端でのウェーブレットを処理する方法をつたえるものです）と共にメキシカンハットウェーブレットを用います。

  for i = 0:19
  	pixels(i+1) = i;
  end
  for i = 1:4
  	scales(i) = 2^i;
  end
  [coeffs] = img.cwt(scales, pixels, 'MexicanHat', 'Zero');

連続ウェーブレット変換はデータ内のピークの解析に用いることが出来ます。この分析の結果、追加のピーク選択制約を指定することができます。これを行うには関数 img.setLimits を用います。

主成分解析

m × n データ行列は、n 次元空間のm点（1 点が 1 ピクセルに対応）の集合として抽象化されたものと見ることが出来ます。すると各ピクセルは、n を飛行時間チャネル数とした n 次元ベクトルとして表現できます。こうして n 軸群上にこれらの点をプロットすることをイメージできます。主成分分析は、点の位置の最大の広がりが第1の軸に沿って生じ、次に第２の軸に沿って最大、などと続くような新しい軸の集合を見つける事が出来ます。

これは２次元では可視化が容易で、以下の赤線が変換後の軸を示します：

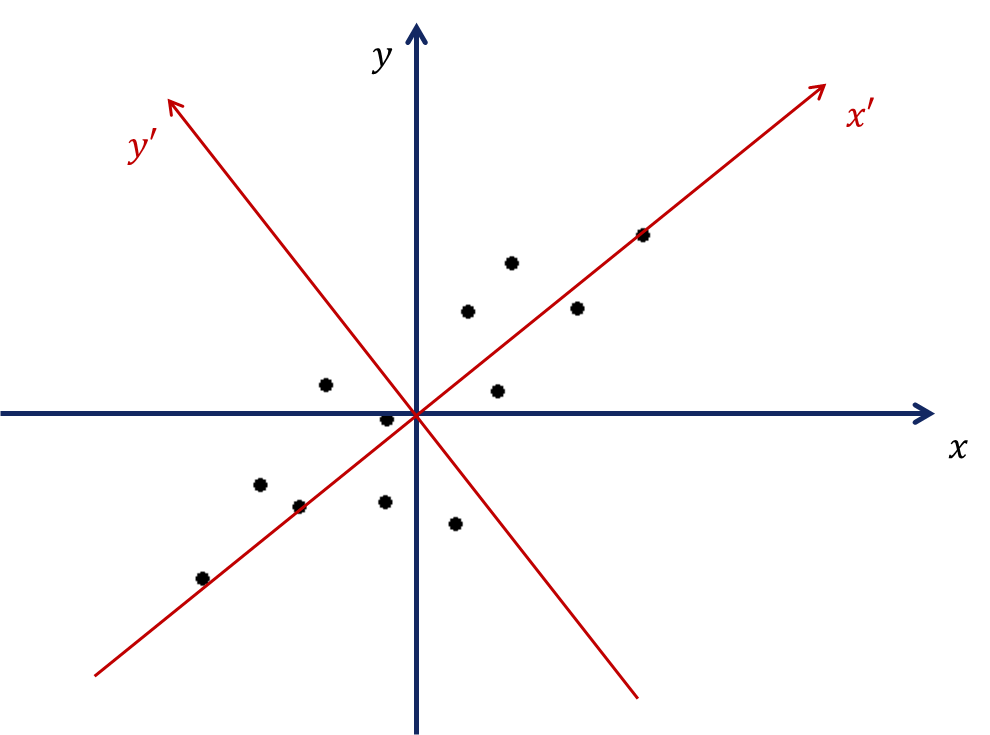
２次元データの主成分分析

新しい軸はローディング、ローディングへのデータの射影はスコアと呼ばれます。高次元のデータに対しては、新たな軸の多くは無視されます。それは、これらが小さなデータの広がりしか持たないためです。よって PCA は次元縮小のために用いることが出来て、新たなデータ行列はかなり小さくなります（僅かな数の列のみ残ります）。以下の例では最初の 10 次元のみを残しています：

  [loadings, scores, eigs, tot] = img.pca(10);

ベクトル eigs は、PCA 中にデータ行列から構成された共分散行列の固有値を含みます。eigs/tot の計算は、新しい次元毎に考慮される分散の割合の尺度を提供します。

t 分布型確率的近傍埋め込み法（t-distributed stochastic neighbor embedding）

通常 t-SNE と略されますが、これは別の次元縮小の方法です。m × n データ行列を新たな m × k 行列（k << n）へ変換するもので、次元圧縮法（low-dimensional embedding）の１種として知られています。通常は k は 2 か 3 を選択され、つまりデータを RGB の値へ変換するのに用いられるのが一般的です。ここで、主成分解析は線形変換（新たな軸は古い軸の線形結合で表される）でしたが、t-SNE は非線形で、より複雑な多項式による変数間の関係が用いられます。

t-SNE は高次元空間内の近傍の点を一致させようとします。つまりそれらは低次元空間内で接近している事になります。これを行うには、高次元空間および低次元空間における点が互いに接近している確率分布を計算し、確率分布間の差の尺度である Kullback-Liebler 発散として知られる量を反復的に最小化します。典型的には、データ行列を約 20 次元に縮小するためには t-SNE の前に PCA を実行します。

t-SNE のパラメータには多くの選択肢があり、計算速度と精度のトレードオフも検討条件となります。これらパラメータについてはソフトウェアに記載されていますが、詳細については文献：Visualizing Data using t-SNE, Laurens van der Maaten and Geoffrey Hinton, Journal of Machine Learning Research, 9$2008$ 2579-2605, and Accelerating t-SNE using Tree-Based Algorithms, Laurens van der Maaten, Journal of Machine Learning Research, 15$2014$ 1-21 を参照してください。

下記の例では、データを３次元まで縮小し、前節の PCA の結果から開始します。どの程度の頻度でスクリーンに出力するかを指定する verbosity といった、様々なオプションパラメータが指定されています。

  [embedding, kl_divergence, total_iter] = img.tsne(3,'data',scores,'max_iter',100,'verbosity',25);

  ** Info: Reducing 4096 x 10 matrix to 4096 x 3 using t-SNE.
  ** Info: Initial Kullback-Liebler divergence = 22.591861.
  ** Info: t-SNE Iteration 25, Kullback-Liebler divergence = 21.926958.
  ** Info: t-SNE Iteration 50, Kullback-Liebler divergence = 2.572930.
  ** Info: t-SNE Iteration 75, Kullback-Liebler divergence = 1.859599.
  ** Info: t-SNE Iteration 100, Kullback-Liebler divergence = 1.622093.
  ** Info: Exiting after the maximum 100 iterations were completed.
  ** Info: Final Kullback-Liebler divergence: 1.622093.

k 平均クラスタリング

k 平均クラスタリングは、データ行列に含まれる m 個の点を k 個のクラスターへ、各クラスター平均との距離が最小になるように分割します。初期クラスター平均は指定も出来ます。また、標準的な幾何距離かベクトル間の距離算出にコサイン類似度のどちらかを使うことも可能です。以下の例では、SpecImage コンストラクタを用いて PCA スコアから新たなイメージを生成して、k = 4 としてデフォルトの幾何距離とランダム初期クラスター平均を用いたk平均クラスタリングを実行します。ただし SpecImage コンストラクタを用いるにはスコア行列の転置（'）が必要です。

  img2 = SpecImage(scores');
  [cmeans, inc, nic, wcs] = img2.kmeans(4);

非負値行列因子分解

非負値行列因子分解は、その積が入力行列 A を近似する２つの行列 W と H を算出する手法です。この時、A は無論、W と H の行列要素は非負値で、その次元はそれぞれ m × k、k × n です。ここでkはユーザが指定する小さな次元数です：

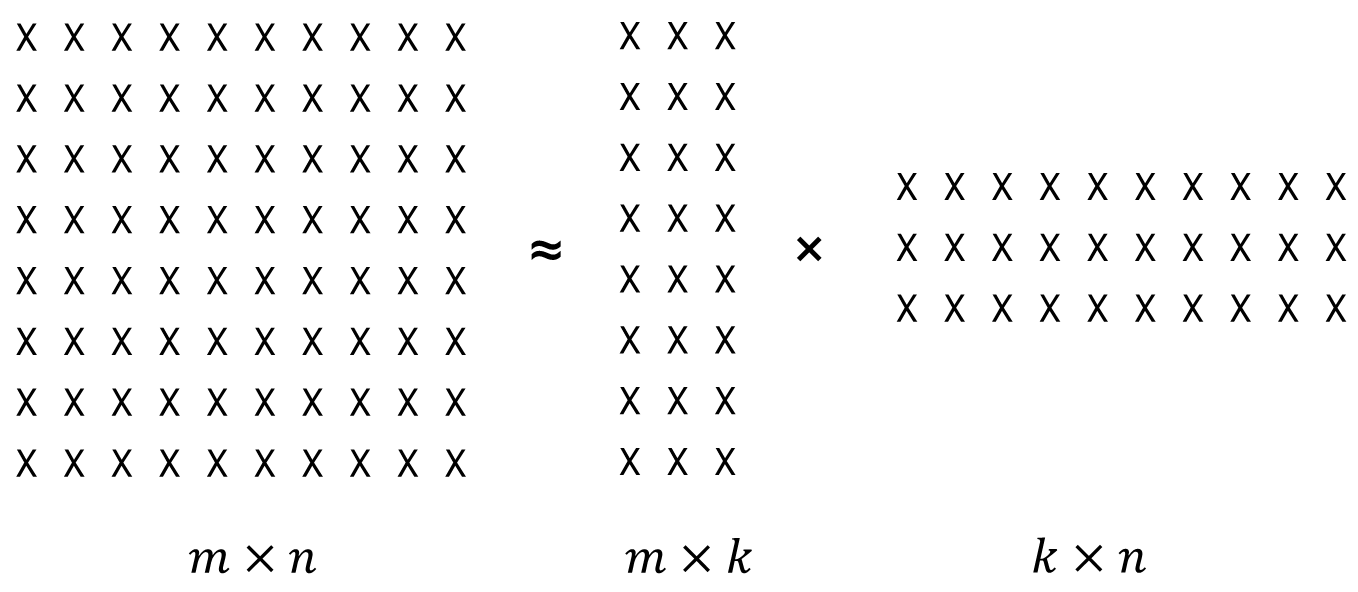
非負値行列因子分解は、一つの行列を短い次元と長い次元数を持つ縦棒と横棒のような２つの行列に分解する

行列 W は基底行列（features matrix）、H は係数行列とも呼ばれます。以下の例では k = 50 として非負値行列因子分解を実行します。

  [W,H] = img.nmf(50);

結果

以下のプロットは、解析ルーチンからの出力を示しています。最初の２つは主成分解析、次に t-SNE を使用した３次元への縮小、４つのクラスターによる k 平均クラスタリング、および非負値行列因子分解の出力です。

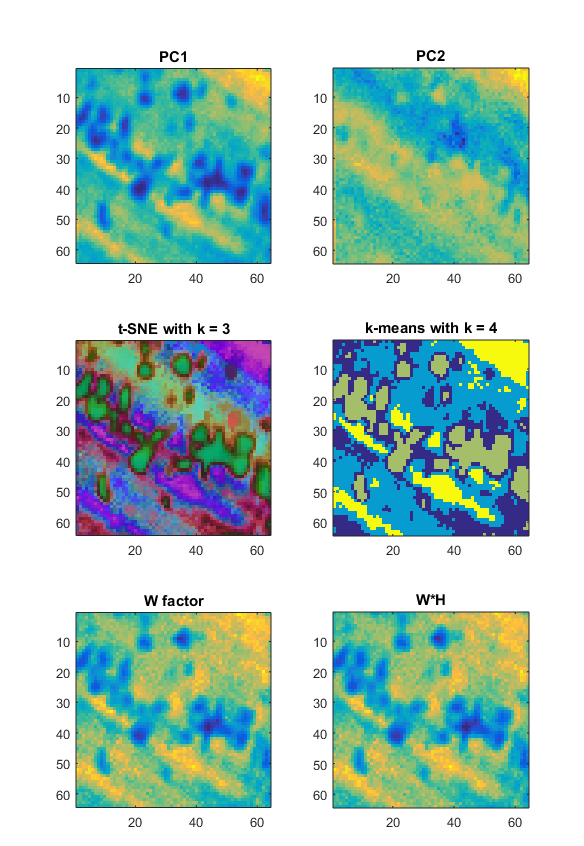
nAG/NPL データ解析ルーチンのプロット

より詳しい情報について

nAG/NPL ハイパースペクトルイメージング・ライブラリは、英国国立物理学研究所：National Physical Laboratory $NPL$, National Centre of Excellence in Mass Spectrometry Imaging $NiCE-MSI$ との２年間にわたる共同作業の成果です。このプロジェクトは Innovate UK の資金で実施されました。

このライブラリーの計算カーネルは C 言語で記述され、一部は nAG ライブラリの Fortran コードが用いられており、並列処理には OpenMP が使用されています。最上位レベルは C++ および MATLAB^® のクラスで記述されています。

このライブラリーには包括的なドキュメント、C++ と MATLAB^® による例題が備わり、MATLAB^® のヘルプシステムに全て組み込まれています。C++ に関する文書は online で閲覧できます。

また、64-bit Windows 向けのビルドが可能で、24 コアで良好なスケール性を示しています。これらのソフトウェアは NPL's internal image fusion software にも組み込まれました。

さらに詳細をお知りになりたい方は コンサルティングサービスのお問い合わせ にご記入の上お問い合わせください。