Keyword: Ridge, リッジ, パラメータ, 回帰
概要
本サンプルはユーザ提供のRidge回帰パラメータを用いたRidge回帰の計算を行うFortranによるサンプルプログラムです。 本サンプルは以下に示されるデータについてRidge回帰の計算を行います。
※本サンプルはnAG Fortranライブラリに含まれるルーチン g02kbf() のExampleコードです。本サンプル及びルーチンの詳細情報は g02kbf のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
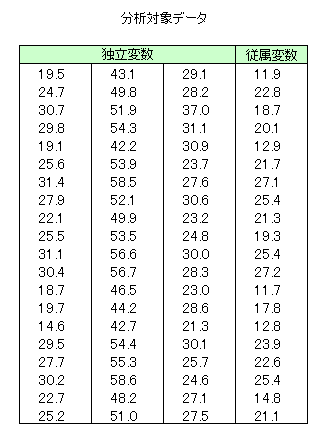
入力データ
（本ルーチンの詳細はg02kbf のマニュアルページを参照）1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
| このデータをダウンロード |
G02KBF Example Program Data 20 3 16 5 1 1 : N, M, LH, LPEC, WANTB, WANTVF L G U F B : PEC 19.5 43.1 29.1 11.9 24.7 49.8 28.2 22.8 30.7 51.9 37.0 18.7 29.8 54.3 31.1 20.1 19.1 42.2 30.9 12.9 25.6 53.9 23.7 21.7 31.4 58.5 27.6 27.1 27.9 52.1 30.6 25.4 22.1 49.9 23.2 21.3 25.5 53.5 24.8 19.3 31.1 56.6 30.0 25.4 30.4 56.7 28.3 27.2 18.7 46.5 23.0 11.7 19.7 44.2 28.6 17.8 14.6 42.7 21.3 12.8 29.5 54.4 30.1 23.9 27.7 55.3 25.7 22.6 30.2 58.6 24.6 25.4 22.7 48.2 27.1 14.8 25.2 51.0 27.5 21.1 : End of observations 1 1 1 : ISX 0.0 0.002 0.004 0.006 0.008 0.010 0.012 0.014 0.016 0.018 0.020 0.022 0.024 0.026 0.028 0.030 : Ridge co-efficients
- １行目はタイトル行で読み飛ばされます。
- ２行目は観測値の数（n=20）、データ行列で有効な独立変数の数（m=3）、提供されたRidgeパラメータの数（lh=16）、予想誤差統計量の数（lpec=5）、パラメータ推定のオプション（wantb=1:元データに対し計算される）、分散拡大要因のオプション（wantvf=1:分散拡大要因が計算される）を指定しています。
- ３行目は予測誤差の手法(pec)を指定しています。"L" は Leave-one-out cross-validation、 "G" は Generalized cross-validation、 "U" は Unbiased estimate of variance、 "F" は Future prediction error、 "B" は Bayesian information criterion を意味します。
- ４～２３行目は独立変数の観測値(x)と従属変数の観測値(y)を指定しています。
- ２４行目はどの独立変数がモデルに含まれるか(isx)を指定しています。
- ２５～２８行目はRidge係数(h)を指定しています。
出力結果
（本ルーチンの詳細はg02kbf のマニュアルページを参照）1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89
| この出力例をダウンロード |
G02KBF Example Program Results
Number of parameters used = 4
Effective number of parameters (NEP):
Ridge
Coeff. NEP
0.0000 4.0000
0.0020 3.2634
0.0040 3.1475
0.0060 3.0987
0.0080 3.0709
0.0100 3.0523
0.0120 3.0386
0.0140 3.0278
0.0160 3.0189
0.0180 3.0112
0.0200 3.0045
0.0220 2.9984
0.0240 2.9928
0.0260 2.9876
0.0280 2.9828
0.0300 2.9782
Parameter Estimates (Original scalings)
Ridge
Coeff. Intercept 1 2 3
0.0000 117.0847 4.3341 -2.8568 -2.1861
0.0020 22.2748 1.4644 -0.4012 -0.6738
0.0040 7.7209 1.0229 -0.0242 -0.4408
0.0060 1.8363 0.8437 0.1282 -0.3460
0.0080 -1.3396 0.7465 0.2105 -0.2944
0.0100 -3.3219 0.6853 0.2618 -0.2619
0.0120 -4.6734 0.6432 0.2968 -0.2393
0.0140 -5.6511 0.6125 0.3222 -0.2228
0.0160 -6.3891 0.5890 0.3413 -0.2100
0.0180 -6.9642 0.5704 0.3562 -0.1999
0.0200 -7.4236 0.5554 0.3681 -0.1916
0.0220 -7.7978 0.5429 0.3779 -0.1847
0.0240 -8.1075 0.5323 0.3859 -0.1788
0.0260 -8.3673 0.5233 0.3926 -0.1737
0.0280 -8.5874 0.5155 0.3984 -0.1693
0.0300 -8.7758 0.5086 0.4033 -0.1653
Variance Inflation Factors
Ridge
Coeff. 1 2 3
0.0000 708.8429 564.3434 104.6060
0.0020 50.5592 40.4483 8.2797
0.0040 16.9816 13.7247 3.3628
0.0060 8.5033 6.9764 2.1185
0.0080 5.1472 4.3046 1.6238
0.0100 3.4855 2.9813 1.3770
0.0120 2.5434 2.2306 1.2356
0.0140 1.9581 1.7640 1.1463
0.0160 1.5698 1.4541 1.0859
0.0180 1.2990 1.2377 1.0428
0.0200 1.1026 1.0805 1.0105
0.0220 0.9556 0.9627 0.9855
0.0240 0.8427 0.8721 0.9655
0.0260 0.7541 0.8007 0.9491
0.0280 0.6832 0.7435 0.9353
0.0300 0.6257 0.6969 0.9235
Prediction error criterion
Ridge
Coeff. 1 2 3 4 5
0.0000 8.0368 7.6879 6.1503 7.3804 8.6052
0.0020 7.5464 7.4238 6.2124 7.2261 8.2355
0.0040 7.5575 7.4520 6.2793 7.2675 8.2515
0.0060 7.5656 7.4668 6.3100 7.2876 8.2611
0.0080 7.5701 7.4749 6.3272 7.2987 8.2661
0.0100 7.5723 7.4796 6.3381 7.3053 8.2685
0.0120 7.5732 7.4823 6.3455 7.3095 8.2695
0.0140 7.5734 7.4838 6.3508 7.3122 8.2696
0.0160 7.5731 7.4845 6.3548 7.3140 8.2691
0.0180 7.5724 7.4848 6.3578 7.3151 8.2683
0.0200 7.5715 7.4847 6.3603 7.3158 8.2671
0.0220 7.5705 7.4843 6.3623 7.3161 8.2659
0.0240 7.5694 7.4838 6.3639 7.3162 8.2645
0.0260 7.5682 7.4832 6.3654 7.3162 8.2630
0.0280 7.5669 7.4825 6.3666 7.3161 8.2615
0.0300 7.5657 7.4818 6.3677 7.3159 8.2600
Key:
1 Leave one out cross-validation
2 Generalised cross-validation
3 Unbiased estimate of variance
4 Final prediction error
5 Bayesian information criterion
- ３行目に使用されたパラメータの数が出力されています。
- ４～２２行目に有効なパラメータの数が出力されています。Ridge係数と有効数が出力されています。
- ２４～４２行目にパラメータ推定値が出力されています。Ridge係数と切片、３種類の予測誤差が出力されています。
- ４４～６２行目に分散拡大要因が出力されています。Ridge係数と３種類の予測誤差が出力されています。
- ６４～８２行目に予測誤差の基準が出力されています。Ridge係数と５種類の予測誤差が出力されています。
- ８４～８９行目に各番号に対応する予測誤差の手法が出力されています。
ソースコード
（本ルーチンの詳細はg02kbf のマニュアルページを参照）
※本サンプルソースコードは科学技術・統計計算ライブラリである「nAG Fortranライブラリ」のルーチンを呼び出します。
サンプルのコンパイル及び実行方法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170
| このソースコードをダウンロード |
PROGRAM g02kbfe
! G02KBF Example Program Text
! Mark 23 Release. nAG Copyright 2011.
! .. Use Statements ..
USE nag_library, ONLY : g02kbf, nag_wp
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Parameters ..
INTEGER, PARAMETER :: nin = 5, nout = 6
! .. Local Scalars ..
INTEGER :: i, ifail, ip, ldb, ldpe, ldvf, ldx, &
lh, lpec, m, n, pl, tdb, tdpe, tdvf, &
wantb, wantvf
! .. Local Arrays ..
REAL (KIND=nag_wp), ALLOCATABLE :: b(:,:), h(:), nep(:), pe(:,:), &
vf(:,:), x(:,:), y(:)
INTEGER, ALLOCATABLE :: isx(:)
CHARACTER (1), ALLOCATABLE :: pec(:)
! .. Intrinsic Functions ..
INTRINSIC count, min
! .. Executable Statements ..
WRITE (nout,*) 'G02KBF Example Program Results'
WRITE (nout,*)
! Skip heading in data file
READ (nin,*)
! Read in the problem size
READ (nin,*) n, m, lh, lpec, wantb, wantvf
ldx = n
ALLOCATE (x(ldx,m),isx(m),y(n),h(lh),pec(lpec))
! Read in data
IF (lpec>0) THEN
READ (nin,*) pec(1:lpec)
END IF
READ (nin,*) (x(i,1:m),y(i),i=1,n)
! Read in variable inclusion flags
READ (nin,*) isx(1:m)
! Read in the ridge coefficients
READ (nin,*) h(1:lh)
! Calculate IP
ip = count(isx(1:m)==1)
IF (wantb/=0) THEN
ldb = ip + 1
tdb = lh
ELSE
ldb = 0
tdb = 0
END IF
IF (wantvf/=0) THEN
ldvf = ip
tdvf = lh
ELSE
ldvf = 0
tdvf = 0
END IF
IF (lpec>0) THEN
ldpe = lpec
tdpe = lh
ELSE
ldpe = 0
tdpe = 0
END IF
ALLOCATE (nep(lh),b(ldb,tdb),vf(ldvf,tdvf),pe(ldpe,tdpe))
! Fit ridge regression
ifail = 0
CALL g02kbf(n,m,x,ldx,isx,ip,y,lh,h,nep,wantb,b,ldb,wantvf,vf,ldvf, &
lpec,pec,pe,ldpe,ifail)
! Display results
WRITE (nout,99994) 'Number of parameters used = ', ip + 1
WRITE (nout,*) 'Effective number of parameters (NEP):'
WRITE (nout,*) ' Ridge '
WRITE (nout,*) ' Coeff. ', 'NEP'
WRITE (nout,99993) (h(i),nep(i),i=1,lh)
! Parameter estimates
IF (wantb/=0) THEN
WRITE (nout,*)
IF (wantb==1) THEN
WRITE (nout,*) 'Parameter Estimates (Original scalings)'
ELSE
WRITE (nout,*) 'Parameter Estimates (Standarised)'
END IF
pl = min(ip,4)
WRITE (nout,*) ' Ridge '
WRITE (nout,99997) ' Coeff. ', ' Intercept ', (i,i=1,pl)
IF (pl<ip-1) THEN
WRITE (nout,99996) (i,i=pl+1,ip-1)
END IF
pl = min(ip+1,5)
DO i = 1, lh
WRITE (nout,99999) h(i), b(1:pl,i)
IF (pl<ip) THEN
WRITE (nout,99998) b((pl+1):ip,i)
END IF
END DO
END IF
! Variance inflation factors
IF (wantvf/=0) THEN
WRITE (nout,*)
WRITE (nout,*) 'Variance Inflation Factors'
pl = min(ip,5)
WRITE (nout,*) ' Ridge '
WRITE (nout,99995) ' Coeff. ', (i,i=1,pl)
IF (pl<ip) THEN
WRITE (nout,99996) (i,i=pl+1,ip)
END IF
DO i = 1, lh
WRITE (nout,99999) h(i), vf(1:pl,i)
IF (pl<ip) THEN
WRITE (nout,99998) vf((pl+1):ip,i)
END IF
END DO
END IF
! Prediction error criterion
IF (lpec>0) THEN
WRITE (nout,*)
WRITE (nout,*) 'Prediction error criterion'
pl = min(lpec,5)
WRITE (nout,*) ' Ridge '
WRITE (nout,99995) ' Coeff. ', (i,i=1,pl)
IF (pl<lpec) THEN
WRITE (nout,99996) (i,i=pl+1,lpec)
END IF
DO i = 1, lh
WRITE (nout,99999) h(i), pe(1:pl,i)
IF (pl<ip) THEN
WRITE (nout,99998) pe((pl+1):ip,i)
END IF
END DO
WRITE (nout,*)
WRITE (nout,*) 'Key:'
DO i = 1, lpec
SELECT CASE (pec(i))
CASE ('L')
WRITE (nout,99992) i, 'Leave one out cross-validation'
CASE ('G')
WRITE (nout,99992) i, 'Generalised cross-validation'
CASE ('U')
WRITE (nout,99992) i, 'Unbiased estimate of variance'
CASE ('F')
WRITE (nout,99992) i, 'Final prediction error'
CASE ('B')
WRITE (nout,99992) i, 'Bayesian information criterion'
END SELECT
END DO
END IF
99999 FORMAT (1X,F10.4,5F10.4)
99998 FORMAT (1X,10X,5F10.4)
99997 FORMAT (1X,A,A,4I10)
99996 FORMAT (10X,5I10)
99995 FORMAT (1X,A,5I10)
99994 FORMAT (1X,A,I10)
99993 FORMAT (1X,F10.4,F10.4)
99992 FORMAT (1X,1X,I5,1X,A)
END PROGRAM g02kbfe