Keyword: 実連立線形方程式
概要
本サンプルは実連立線形方程式の解を求めるFortranによるサンプルプログラムです。 本サンプルはAとBが以下に示される場合の実連立線形方程式 AX=B の解を求めて出力します。
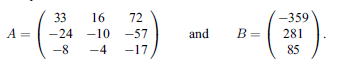
※本サンプルはnAG Fortranライブラリに含まれるルーチン f04ajf() のExampleコードです。本サンプル及びルーチンの詳細情報は f04ajf のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
（本ルーチンの詳細はf04ajf のマニュアルページを参照）1 2 3 4 5 6
| このデータをダウンロード |
F04AJF Example Program Data 3 : n 33 16 72 -24 -10 -57 -8 -4 -17 -359 281 85 : matrices A and B
- １行目はタイトル行で読み飛ばされます。
- ２行目に行列Aの次数(n)を指定しています。
- ３～５行目に行列Aの要素を指定しています。
- ６行目に行列Bの要素を指定しています。
出力結果
（本ルーチンの詳細はf04ajf のマニュアルページを参照）- ３～６行目にxの解が出力されています。
ソースコード
（本ルーチンの詳細はf04ajf のマニュアルページを参照）
※本サンプルソースコードは科学技術・統計計算ライブラリである「nAG Fortranライブラリ」のルーチンを呼び出します。
サンプルのコンパイル及び実行方法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47
| このソースコードをダウンロード |
PROGRAM f04ajfe
! F04AJF Example Program Text
! Mark 23 Release. nAG Copyright 2011.
! .. Use Statements ..
USE nag_library, ONLY : f03aff, f04ajf, nag_wp
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Parameters ..
INTEGER, PARAMETER :: nin = 5, nout = 6
! .. Local Scalars ..
REAL (KIND=nag_wp) :: d1, eps
INTEGER :: i, id, ifail, ir, lda, ldb, n
! .. Local Arrays ..
REAL (KIND=nag_wp), ALLOCATABLE :: a(:,:), b(:,:), p(:)
! .. Executable Statements ..
WRITE (nout,*) 'F04AJF Example Program Results'
WRITE (nout,*)
! Skip heading in data file
READ (nin,*)
READ (nin,*) n
ir = 1
lda = n
ldb = n
ALLOCATE (a(lda,n),b(ldb,ir),p(n))
READ (nin,*) (a(i,1:n),i=1,n)
! ifail: behaviour on error exit
! =0 for hard exit, =1 for quiet-soft, =-1 for noisy-soft
ifail = 0
! Crout decomposition
CALL f03aff(n,eps,a,lda,d1,id,p,ifail)
READ (nin,*) (b(i,1:ir),i=1,n)
! Approximate solution of linear equations
CALL f04ajf(n,ir,a,lda,p,b,ldb)
WRITE (nout,*) ' Solution'
DO i = 1, n
WRITE (nout,99999) b(i,1:ir)
END DO
99999 FORMAT (1X,8F9.4)
END PROGRAM f04ajfe