Keyword: 一様準乱数列
概要
本サンプルは一様準乱数列の生成を行うFortranによるサンプルプログラムです。 本サンプルは一様準乱数列を生成し以下に示される積分を推定し出力します。
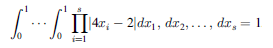
※本サンプルはnAG Fortranライブラリに含まれるルーチン g05ymf() のExampleコードです。本サンプル及びルーチンの詳細情報は g05ymf のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
（本ルーチンの詳細はg05ymf のマニュアルページを参照）- １行目はタイトル行で読み飛ばされます。
- ２行目に使用する生成器（genid=1:Sobol生成器）を指定しています。
- ３行目に必要とする準乱数の数（n=200）、次元数（idim=8）、生成器の初期化でスキップする数列の項数（iskip=1000）を指定しています。
- ４行目に表示する変量の数(dn)を指定しています。
出力結果
（本ルーチンの詳細はg05ymf のマニュアルページを参照）1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
| この出力例をダウンロード |
G05YMF Example Program Results
Value of integral = 1.0410
First 5 variates for all 8 dimensions
1 2 3 4 5
1 0.7197 0.9697 0.4697 0.3447 0.8447
2 0.5967 0.3467 0.8467 0.4717 0.9717
3 0.0186 0.7686 0.2686 0.1436 0.6436
4 0.1768 0.9268 0.4268 0.3018 0.8018
5 0.7803 0.5303 0.0303 0.1553 0.6553
6 0.4072 0.1572 0.6572 0.7822 0.2822
7 0.5459 0.2959 0.7959 0.4209 0.9209
8 0.3994 0.1494 0.6494 0.0244 0.5244
- ４行目に推定された積分の値が出力されています。
- ７～１５行目に生成された一様準乱数列の最初の５つの変量が出力されています。
ソースコード
（本ルーチンの詳細はg05ymf のマニュアルページを参照）
※本サンプルソースコードは科学技術・統計計算ライブラリである「nAG Fortranライブラリ」のルーチンを呼び出します。
サンプルのコンパイル及び実行方法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116
| このソースコードをダウンロード |
! G05YMF Example Program Text
! Mark 23 Release. nAG Copyright 2011.
MODULE g05ymfe_mod
! G05YMF Example Program Module:
! Parameters and User-defined Routines
! .. Use Statements ..
USE nag_library, ONLY : nag_wp
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Parameters ..
INTEGER, PARAMETER :: nin = 5, nout = 6
CONTAINS
FUNCTION ifun(x,lx)
! Function being integrated, in this example
! ABS(4.0 X - 2)
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Function Return Value ..
REAL (KIND=nag_wp) :: ifun
! .. Scalar Arguments ..
INTEGER, INTENT (IN) :: lx
! .. Array Arguments ..
REAL (KIND=nag_wp), INTENT (IN) :: x(lx)
! .. Local Scalars ..
INTEGER :: d
! .. Intrinsic Functions ..
INTRINSIC abs
! .. Executable Statements ..
ifun = 1.0E0_nag_wp
DO d = 1, lx
ifun = ifun*abs(4.0E0_nag_wp*x(d)-2.0E0_nag_wp)
END DO
END FUNCTION ifun
END MODULE g05ymfe_mod
PROGRAM g05ymfe
! G05YMF Example Main Program
! .. Use Statements ..
USE nag_library, ONLY : g05ylf, g05ymf, nag_wp, x04caf
USE g05ymfe_mod, ONLY : ifun, nin, nout
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Local Scalars ..
REAL (KIND=nag_wp) :: sum, vsbl
INTEGER :: dn, genid, i, idim, ifail, &
iskip, ldquas, liref, n, rcord
CHARACTER (80) :: title
! .. Local Arrays ..
REAL (KIND=nag_wp), ALLOCATABLE :: quas(:,:)
INTEGER, ALLOCATABLE :: iref(:)
! .. Intrinsic Functions ..
INTRINSIC real
! .. Executable Statements ..
WRITE (nout,*) 'G05YMF Example Program Results'
WRITE (nout,*)
! Skip heading in data file
READ (nin,*)
! Fix the RCORD = 1, so QUAS(IDIM,N). As we
! are accessing each dimension in turn for a given variate
! when evaluating the function, this is more efficient
rcord = 1
! Read in the generator to use
READ (nin,*) genid
! Read in the problem size
READ (nin,*) n, idim, iskip
IF (genid==4) THEN
liref = 407
ELSE
liref = 32*idim + 7
END IF
ldquas = idim
ALLOCATE (quas(ldquas,n),iref(liref))
! Initialize the generator
ifail = 0
CALL g05ylf(genid,idim,iref,liref,iskip,ifail)
! Generate N quasi-random variates
ifail = 0
CALL g05ymf(n,rcord,quas,ldquas,iref,ifail)
! Evaluate the function, and sum
sum = 0.0E0_nag_wp
DO i = 1, n
sum = sum + ifun(quas(1:idim,i),idim)
END DO
! Convert sum to mean value
vsbl = sum/real(n,kind=nag_wp)
WRITE (nout,*)
WRITE (nout,99999) 'Value of integral = ', vsbl
! Read in number of variates to display
READ (nin,*) dn
! Display the first DN variates
WRITE (nout,*)
WRITE (title,99998) 'First ', dn, ' variates for all ', idim, &
' dimensions'
FLUSH (nout)
ifail = 0
CALL x04caf('General',' ',idim,dn,quas,ldquas,title,ifail)
99999 FORMAT (1X,A,F8.4)
99998 FORMAT (A,I0,A,I0,A)
END PROGRAM g05ymfe