多次元尺度構成法の計算

ホーム > 製品 > nAG数値計算ライブラリ > nAG Fortranライブラリ > サンプルソースコード集 > 多次元尺度構成法の計算

Keyword: 多次元尺度, 構成法, 計算, 多変量解析

概要

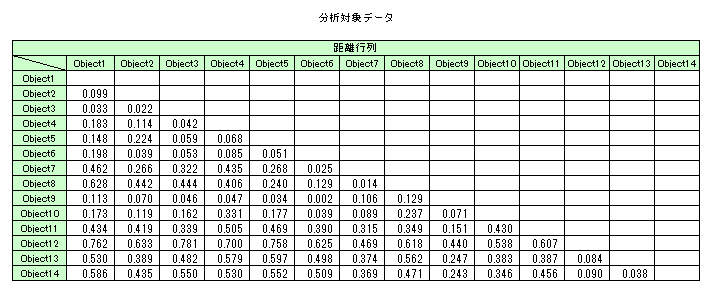
本サンプルは多次元尺度構成法の計算を行うFortranによるサンプルプログラムです。本サンプルは以下に示される距離行列について多次元尺度構成法の計算を行います。

多次元尺度構成法のデータ　

※本サンプルはnAG Fortranライブラリに含まれるルーチン g03fcf() のExampleコードです。本サンプル及びルーチンの詳細情報は g03fcf のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで

入力データ

このデータをダウンロード

G03FCF Example Program Data
14 2 'L' 'T'                                                   :N,NDIM,ROOTS,TYP
0.099
0.033 0.022
0.183 0.114 0.042
0.148 0.224 0.059 0.068
0.198 0.039 0.053 0.085 0.051
0.462 0.266 0.322 0.435 0.268 0.025
0.628 0.442 0.444 0.406 0.240 0.129 0.014
0.113 0.070 0.046 0.047 0.034 0.002 0.106 0.129
0.173 0.119 0.162 0.331 0.177 0.039 0.089 0.237 0.071
0.434 0.419 0.339 0.505 0.469 0.390 0.315 0.349 0.151 0.430
0.762 0.633 0.781 0.700 0.758 0.625 0.469 0.618 0.440 0.538 0.607
0.530 0.389 0.482 0.579 0.597 0.498 0.374 0.562 0.247 0.383 0.387 0.084
0.586 0.435 0.550 0.530 0.552 0.509 0.369 0.471 0.234 0.346 0.456 0.090 0.038 :D

１行目はタイトル行で読み飛ばされます。
２行目には距離行列のオブジェクト数（n=14）、データを表すのに使用される次元の数（ndim=2）、全ての固有値が計算されるか最大次元数の固有値のみ計算されるか（roots='L':最大次元数の固有値のみ）、ストレス（STRESS）と平方ストレス（sstress）のどちらが使用されるか（typ='T':STRESSが使用される）を指定しています。
３～１５行目に下三角の距離行列(d)を指定しています。

出力結果

（本ルーチンの詳細はg03fcf のマニュアルページを参照）

この出力例をダウンロード

 G03FCF Example Program Results

          STRESS =    0.1256E+00

 Co-ordinates
           1       2
  1   0.2060  0.2438
  2   0.1063  0.1418
  3   0.2224  0.0817
  4   0.3032  0.0355
  5   0.2645 -0.0698
  6   0.1554 -0.0435
  7  -0.0070 -0.1612
  8   0.0749 -0.3275
  9   0.0488  0.0289
 10   0.0124 -0.0267
 11  -0.1649 -0.2500
 12  -0.5073  0.1267
 13  -0.3093  0.1590
 14  -0.3498  0.0700

  Plot of first two dimensions

            +....+....+....+....+....+....+....+....+....+....+.
            .                             .                    .
            .                             .                    .
            .                             .         1          .
       0.200+                             +                    +
            .              1              .    1               .
            .    1                        .                    .
            .            1                .          1         .
            .                             . 1            1     .
       0.000+....+....+....+....+....+....+....+....+....+....++
            .                             .1      1            .
            .                             .            1       .
            .                             .                    .
            .                             1                    .
      -0.200+                             +                    +
            .                     1       .                    .
            .                             .                    .
            .                             .   1                .
            .                             .                    .
      -0.400+....+....+....+....+....+....+....+....+....+....+.
           -.6000    -.4000    -.2000    0.0000    0.2000    0.4000
                -.5000    -.3000    -.1000    0.1000    0.3000

３行目にストレスの値が出力されています。
５～２０行目には座標が出力されています。
２２～４５行目にはプロット図が出力されています。

ソースコード

（本ルーチンの詳細はg03fcf のマニュアルページを参照）

※本サンプルソースコードは科学技術・統計計算ライブラリである「nAG Fortranライブラリ」のルーチンを呼び出します。
サンプルのコンパイル及び実行方法

このソースコードをダウンロード

    PROGRAM g03fcfe

!      G03FCF Example Program Text

!      Mark 23 Release. nAG Copyright 2011.

!      .. Use Statements ..
       USE nag_library, ONLY : g01agf, g03faf, g03fcf, nag_wp, x04caf
!      .. Implicit None Statement ..
       IMPLICIT NONE
!      .. Parameters ..
       INTEGER, PARAMETER              :: nin = 5, nout = 6
!      .. Local Scalars ..
       REAL (KIND=nag_wp)              :: stress
       INTEGER                         :: ifail, iopt, iter, ld, ldfit, ldx,   &
                                          liwk, lwk, n, ndim
       CHARACTER (1)                   :: roots, typ
!      .. Local Arrays ..
       REAL (KIND=nag_wp), ALLOCATABLE :: d(:), dfit(:), eval(:), wk(:), x(:,:)
       INTEGER, ALLOCATABLE            :: iwk(:)
!      .. Intrinsic Functions ..
       INTRINSIC                          max
!      .. Executable Statements ..
       WRITE (nout,*) 'G03FCF Example Program Results'
       WRITE (nout,*)

!      Skip heading in data file
       READ (nin,*)

!      Read in the problem size
       READ (nin,*) n, ndim, roots, typ

       ld = n*(n-1)/2
       ldx = n
       lwk = max(n*(n+17)/2-1,15*n*ndim)
       liwk = max(5*n,n*(n-1)/2+n*ndim+5)
       ldfit = 2*n*(n-1)
       ALLOCATE (d(ld),x(ldx,ndim),eval(n),wk(lwk),iwk(liwk),dfit(ldfit))

!      Read in the lower triangular part of the distance matrix
       READ (nin,*) d(1:ld)

!      Perform principal co-ordinate analysis
       ifail = 0
       CALL g03faf(roots,n,d,ndim,x,ldx,eval,wk,iwk,ifail)

!      Use default values for number of iterations and options
       iter = 0
       iopt = 0

!      Perform multi-dimensional scaling
       ifail = 0
       CALL g03fcf(typ,n,ndim,d,x,ldx,stress,dfit,iter,iopt,wk,iwk,ifail)

!      Display the results
       WRITE (nout,99999) 'STRESS = ', stress
       WRITE (nout,*)
       FLUSH (nout)
       ifail = 0
       CALL x04caf('General',' ',n,ndim,x,ldx,'Co-ordinates',ifail)
       WRITE (nout,*)
       WRITE (nout,*) ' Plot of first two dimensions'
       WRITE (nout,*)
       FLUSH (nout)
       ifail = 0
       CALL g01agf(x(1,1),x(1,2),n,iwk,50,18,ifail)

99999  FORMAT (10X,A,E13.4)
    END PROGRAM g03fcfe

Fortranによるサンプルソースコード : 使用ルーチン名：g03fcf

概要

入力データ

出力結果

ソースコード