一般化線形モデルの推定可能関数とその標準誤差の計算

ホーム > 製品 > nAG数値計算ライブラリ > nAG Fortranライブラリ > サンプルソースコード集 > 一般化線形モデルの推定可能関数とその標準誤差の計算

Keyword: 一般化線形モデル, 推定可能関数, 標準誤差

概要

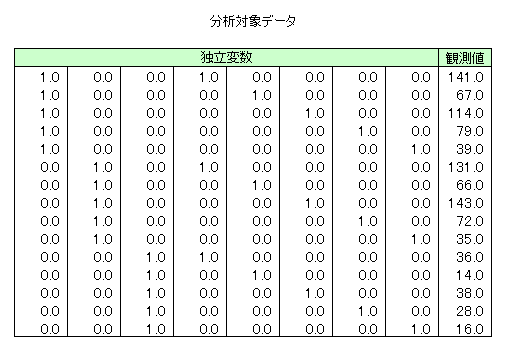
本サンプルは一般化線形モデルの推定可能関数とその標準誤差の計算を行うFortranによるサンプルプログラムです。本サンプルは以下に示されるデータについて推定可能関数とその標準誤差の計算を行います。

一般化線形モデルのフィットのデータ　

※本サンプルはnAG Fortranライブラリに含まれるルーチン g02gnf() のExampleコードです。本サンプル及びルーチンの詳細情報は g02gnf のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで

入力データ

このデータをダウンロード

G02GNF Example Program Data
'L' 'M' 'N' 'U'  15 8                  :: LINK,MEAN,OFFSET,WEIGHT,N,M
1.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 141.0
1.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0  67.0
1.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 114.0
1.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0  79.0
1.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0  39.0
0.0 1.0 0.0 1.0 0.0 0.0 0.0 0.0 131.0
0.0 1.0 0.0 0.0 1.0 0.0 0.0 0.0  66.0
0.0 1.0 0.0 0.0 0.0 1.0 0.0 0.0 143.0
0.0 1.0 0.0 0.0 0.0 0.0 1.0 0.0  72.0
0.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0  35.0
0.0 0.0 1.0 1.0 0.0 0.0 0.0 0.0  36.0
0.0 0.0 1.0 0.0 1.0 0.0 0.0 0.0  14.0
0.0 0.0 1.0 0.0 0.0 1.0 0.0 0.0  38.0
0.0 0.0 1.0 0.0 0.0 0.0 1.0 0.0  28.0
0.0 0.0 1.0 0.0 0.0 0.0 0.0 1.0  16.0   :: End of X, Y
 1   1   1   1   1   1   1   1          :: ISX
 0  1.0E-6  5.0E-5  0                   :: IPRINT,EPS,TOL,MAXIT
 1.0  1.0  0.0 0.0  1.0 0.0 0.0 0.0 0.0 :: Estimable function 1 (F)
 0.0  1.0 -1.0 0.0  0.0 0.0 0.0 0.0 0.0 :: Estimable function 2 (F)
 0.0  1.0  0.0 0.0  0.0 0.0 0.0 0.0 0.0 :: Estimable function 3 (F)

１行目はタイトル行で読み飛ばされます。
２行目はどのリンク関数が使用されるか（link='L':ログリンク）、一般化線形モデルの引数に切片が含まれるかどうか（mean='M':切片を含める）、オフセットが必要かどうか（offset='N':不要）、重みづけをするかどうかどうか（weight='U':重みづけをしない）、観測値の数（n=15）、独立変数の数（m=8）を指定しています。
３～１７行目に独立変数の観測値(x)と従属変数の観測値(y)を指定しています。
１８行目はモデルに独立変数が含まれるかどうか(isx)を指定しています。"1"は含まれることを意味します。
１９行目は反復の情報の出力が必要かどうか（iprint=0:不要）、独立変数がフルランクかどうかそうでない場合ランクは何か（eps=1.0E-6）、モデルのフィットに必要な正確さ（tol=5.0E-5）、最大反復数（maxit=0:デフォルト値10を使用）を指定しています。
２０～２２行目は推定される線形関数(f)を指定しています。

出力結果

（本ルーチンの詳細はg02gnf のマニュアルページを参照）

この出力例をダウンロード

 G02GNF Example Program Results

 Deviance =   0.9038E+01
 Degrees of freedom =  8

       Estimate     Standard error

         2.5977        0.0258
         1.2619        0.0438
         1.2777        0.0436
         0.0580        0.0668
         1.0307        0.0551
         0.2910        0.0732
         0.9876        0.0559
         0.4880        0.0675
        -0.1996        0.0904

 Function    1
     1.00    1.00    0.00    0.00    1.00
     0.00    0.00    0.00    0.00

 STAT =     4.8903 SE =     0.0674 Z =    72.5934

 Function    2
     0.00    1.00   -1.00    0.00    0.00
     0.00    0.00    0.00    0.00

 STAT =    -0.0158 SE =     0.0672 Z =    -0.2350

 Function    3
     0.00    1.00    0.00    0.00    0.00
     0.00    0.00    0.00    0.00

 Function not estimable

３行目にデビアンス（deviance）が出力されています。
４行目に自由度が出力されています。
６～１６行目に一般化線形モデルの引数の推定値と標準誤差が出力されています。
１８～２０行目に１つ目の推定される線形関数が出力されています。
２２行目に関数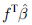の推定値、関数 se(F)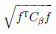（）の推定値の標準誤差、ゼロに等しい関数の検証のためのZ統計量が出力されています。
２４～２６行目に２つ目の推定される線形関数が出力されています。
２８行目に関数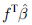の推定値、関数 se(F)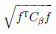（）の推定値の標準誤差、ゼロに等しい関数の検証のためのZ統計量が出力されています。
３０～３２行目に３つめの推定される線形関数が出力されています。
３４行目に関数が推定可能ではないことが表示されています。

ソースコード

（本ルーチンの詳細はg02gnf のマニュアルページを参照）

※本サンプルソースコードは科学技術・統計計算ライブラリである「nAG Fortranライブラリ」のルーチンを呼び出します。
サンプルのコンパイル及び実行方法

このソースコードをダウンロード

    PROGRAM g02gnfe

!      G02GNF Example Program Text

!      Mark 23 Release. nAG Copyright 2011.

!      .. Use Statements ..
       USE nag_library, ONLY : g02gcf, g02gnf, nag_wp
!      .. Implicit None Statement ..
       IMPLICIT NONE
!      .. Parameters ..
       INTEGER, PARAMETER              :: nin = 5, nout = 6
!      .. Local Scalars ..
       REAL (KIND=nag_wp)              :: a, dev, eps, sestat, stat, tol, z
       INTEGER                         :: i, idf, ifail, ip, iprint, irank,    &
                                          ldv, ldx, lwk, lwt, m, maxit, n
       LOGICAL                         :: est
       CHARACTER (1)                   :: link, mean, offset, weight
!      .. Local Arrays ..
       REAL (KIND=nag_wp), ALLOCATABLE :: b(:), cov(:), f(:), se(:), v(:,:),   &
                                          wk(:), wt(:), x(:,:), y(:)
       INTEGER, ALLOCATABLE            :: isx(:)
!      .. Intrinsic Functions ..
       INTRINSIC                          count, max
!      .. Executable Statements ..
       WRITE (nout,*) 'G02GNF Example Program Results'
       WRITE (nout,*)

!      Skip heading in data file
       READ (nin,*)

!      Read in the problem size
       READ (nin,*) link, mean, offset, weight, n, m

       IF (weight=='W' .OR. weight=='w') THEN
          lwt = n
       ELSE
          lwt = 0
       END IF
       ldx = n
       ALLOCATE (x(ldx,m),y(n),wt(lwt),isx(m))

!      Read in data
       IF (lwt>0) THEN
          READ (nin,*) (x(i,1:m),y(i),wt(i),i=1,n)
       ELSE
          READ (nin,*) (x(i,1:m),y(i),i=1,n)
       END IF

!      Read in variable inclusion flags
       READ (nin,*) isx(1:m)

!      Calculate IP
       ip = count(isx(1:m)>0)
       IF (mean=='M' .OR. mean=='m') THEN
          ip = ip + 1
       END IF

!      Read in power for exponential link
       IF (link=='E' .OR. link=='e') THEN
          READ (nin,*) a
       END IF

       ldv = n
       lwk = max((ip*ip+3*ip+22)/2,ip)
       ALLOCATE (b(ip),se(ip),cov(ip*(ip+1)/2),v(ldv,ip+7),wk(lwk),f(ip))

!      Read in the offset
       IF (offset=='Y' .OR. offset=='y') THEN
          READ (nin,*) v(1:n,7)
       END IF

!      Read in control parameters
       READ (nin,*) iprint, eps, tol, maxit

!      Fit generalized linear model with Poisson errors
       ifail = -1
       CALL g02gcf('L','M','N','U',n,x,ldx,m,isx,ip,y,wt,a,dev,idf,b,irank,se, &
          cov,v,ldv,tol,maxit,iprint,eps,wk,ifail)
       IF (ifail/=0) THEN
          IF (ifail<7) THEN
             GO TO 20
          END IF
       END IF

!      Display initial results
       WRITE (nout,99999) 'Deviance = ', dev
       WRITE (nout,99998) 'Degrees of freedom = ', idf
       WRITE (nout,*)
       WRITE (nout,*) '      Estimate     Standard error'
       WRITE (nout,*)
       WRITE (nout,99997) (b(i),se(i),i=1,ip)

!      Estimate the estimable functions
       i = 0
FUN_LP: DO
!         Read in the function
          READ (nin,*,IOSTAT=ifail) f(1:ip)
          IF (ifail/=0) THEN
             EXIT FUN_LP
          END IF

          i = i + 1

!         Estimate it
          ifail = -1
          CALL g02gnf(ip,irank,b,cov,v,ldv,f,est,stat,sestat,z,tol,wk,ifail)
          IF (ifail/=0) THEN
             IF (ifail/=2) THEN
                GO TO 20
             END IF
          END IF

!         Display results
          WRITE (nout,*)
          WRITE (nout,99996) 'Function ', i
          WRITE (nout,99995) f(1:ip)
          WRITE (nout,*)
          IF (est) THEN
             WRITE (nout,99994) 'STAT = ', stat, ' SE = ', sestat, ' Z = ', z
          ELSE
             WRITE (nout,*) 'Function not estimable'
          END IF
       END DO FUN_LP

20     CONTINUE

99999  FORMAT (1X,A,E12.4)
99998  FORMAT (1X,A,I2)
99997  FORMAT (1X,2F14.4)
99996  FORMAT (1X,A,I4)
99995  FORMAT (1X,5F8.2)
99994  FORMAT (1X,A,F10.4,A,F10.4,A,F10.4)
    END PROGRAM g02gnfe

一般化線形モデルの推定可能関数とその標準誤差の計算

Fortranによるサンプルソースコード : 使用ルーチン名：g02gnf

概要

入力データ

出力結果

ソースコード