Keyword: 実行列, ペア, 一般化特異値分解
概要
本サンプルは実行列ペアの一般化特異値分解を行うFortranによるサンプルプログラムです。 本サンプルは以下に示される実行列ペアの一般化特異値分解を行い、条件数の推定値と一般化特異値の誤差推定値を出力します。
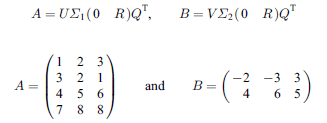
※本サンプルはnAG Fortranライブラリに含まれるルーチン f08vaf() のExampleコードです。本サンプル及びルーチンの詳細情報は f08vaf のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
（本ルーチンの詳細はf08vaf のマニュアルページを参照）1 2 3 4 5 6 7 8 9 10 11
| このデータをダウンロード |
F08VAF Example Program Data 4 3 2 :Values of M, N and P 1.0 2.0 3.0 3.0 2.0 1.0 4.0 5.0 6.0 7.0 8.0 8.0 :End of matrix A -2.0 -3.0 3.0 4.0 6.0 5.0 :End of matrix B
- １行目はタイトル行で読み飛ばされます。
- ３行目に行列Aの行数(m)、行列Aと行列Bの列数(n)、行列Bの行数(p)を指定しています。
- ５～８行目に行列Aの要素を指定しています。
- １０～１１行目に行列Bの要素を指定しています。
出力結果
（本ルーチンの詳細はf08vaf のマニュアルページを参照）1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41
| この出力例をダウンロード |
F08VAF Example Program Results
Number of infinite generalized singular values (K)
1
Number of finite generalized singular values (L)
2
Numerical rank of (A**T B**T)**T (K+L)
3
Finite generalized singular values
1.3151E+00 8.0185E-02
Orthogonal matrix U
1 2 3 4
1 -1.3484E-01 5.2524E-01 -2.0924E-01 8.1373E-01
2 6.7420E-01 -5.2213E-01 -3.8886E-01 3.4874E-01
3 2.6968E-01 5.2757E-01 -6.5782E-01 -4.6499E-01
4 6.7420E-01 4.1615E-01 6.1014E-01 1.5127E-15
Orthogonal matrix V
1 2
1 3.5539E-01 -9.3472E-01
2 9.3472E-01 3.5539E-01
Orthogonal matrix Q
1 2 3
1 -8.3205E-01 -9.4633E-02 -5.4657E-01
2 5.5470E-01 -1.4195E-01 -8.1985E-01
3 0.0000E+00 -9.8534E-01 1.7060E-01
Non singular upper triangular matrix R
1 2 3
1 -2.0569E+00 -9.0121E+00 -9.3705E+00
2 -1.0882E+01 -7.2688E+00
3 -6.0405E+00
Estimate of reciprocal condition number for R
4.2E-02
Error estimate for the generalized singular values
2.6E-15
- ４行目に無限大の一般化特異値の数が出力されています。
- ６行目に有限の一般化特異値の数が出力されています。
- ８行目に行列の有効ランクが出力されています。
- １１行目に有限の一般化特異値が出力されています。
- １４～１８行目に直交行列Uが出力されています。
- ２１～２３行目に直交行列Vが出力されています。
- ２６～２９行目に直交行列Qが出力されています。
- ３２～３５行目に正則上三角行列Rが出力されています。
- ３８行目にRの条件数の逆数の推定値が出力されています。
- ４１行目に一般化特異値の誤差推定が出力されています。
ソースコード
（本ルーチンの詳細はf08vaf のマニュアルページを参照）
※本サンプルソースコードは科学技術・統計計算ライブラリである「nAG Fortranライブラリ」のルーチンを呼び出します。
サンプルのコンパイル及び実行方法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124
| このソースコードをダウンロード |
PROGRAM f08vafe
! F08VAF Example Program Text
! Mark 23 Release. nAG Copyright 2011.
! .. Use Statements ..
USE nag_library, ONLY : dggsvd, dtrcon, nag_wp, x02ajf, x04cbf
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Parameters ..
INTEGER, PARAMETER :: nin = 5, nout = 6
! .. Local Scalars ..
REAL (KIND=nag_wp) :: eps, rcond, serrbd
INTEGER :: i, ifail, info, irank, j, k, l, lda, &
ldb, ldq, ldu, ldv, m, n, p
! .. Local Arrays ..
REAL (KIND=nag_wp), ALLOCATABLE :: a(:,:), alpha(:), b(:,:), beta(:), &
q(:,:), u(:,:), v(:,:), work(:)
INTEGER, ALLOCATABLE :: iwork(:)
CHARACTER (1) :: clabs(1), rlabs(1)
! .. Executable Statements ..
WRITE (nout,*) 'F08VAF Example Program Results'
WRITE (nout,*)
FLUSH (nout)
! Skip heading in data file
READ (nin,*)
READ (nin,*) m, n, p
lda = m
ldb = p
ldq = n
ldu = m
ldv = p
ALLOCATE (a(lda,n),alpha(n),b(ldb,n),beta(n),q(ldq,n),u(ldu,m), &
v(ldv,p),work(m+3*n),iwork(n))
! Read the m by n matrix A and p by n matrix B from data file
READ (nin,*) (a(i,1:n),i=1,m)
READ (nin,*) (b(i,1:n),i=1,p)
! Compute the generalized singular value decomposition of (A, B)
! (A = U*D1*(0 R)*(Q**T), B = V*D2*(0 R)*(Q**T), m>=n)
! The nAG name equivalent of dggsvd is f08vaf
CALL dggsvd('U','V','Q',m,n,p,k,l,a,lda,b,ldb,alpha,beta,u,ldu,v,ldv,q, &
ldq,work,iwork,info)
IF (info==0) THEN
! Print solution
irank = k + l
WRITE (nout,*) 'Number of infinite generalized singular values (K)'
WRITE (nout,99999) k
WRITE (nout,*) 'Number of finite generalized singular values (L)'
WRITE (nout,99999) l
WRITE (nout,*) 'Numerical rank of (A**T B**T)**T (K+L)'
WRITE (nout,99999) irank
WRITE (nout,*)
WRITE (nout,*) 'Finite generalized singular values'
WRITE (nout,99998) (alpha(j)/beta(j),j=k+1,irank)
WRITE (nout,*)
FLUSH (nout)
! ifail: behaviour on error exit
! =0 for hard exit, =1 for quiet-soft, =-1 for noisy-soft
ifail = 0
CALL x04cbf('General',' ',m,m,u,ldu,'1P,E12.4', &
'Orthogonal matrix U','Integer',rlabs,'Integer',clabs,80,0,ifail)
WRITE (nout,*)
FLUSH (nout)
CALL x04cbf('General',' ',p,p,v,ldv,'1P,E12.4', &
'Orthogonal matrix V','Integer',rlabs,'Integer',clabs,80,0,ifail)
WRITE (nout,*)
FLUSH (nout)
CALL x04cbf('General',' ',n,n,q,ldq,'1P,E12.4', &
'Orthogonal matrix Q','Integer',rlabs,'Integer',clabs,80,0,ifail)
WRITE (nout,*)
FLUSH (nout)
CALL x04cbf('Upper triangular','Non-unit',irank,irank, &
a(1,n-irank+1),lda,'1P,E12.4', &
'Non singular upper triangular matrix R','Integer',rlabs, &
'Integer',clabs,80,0,ifail)
! Call DTRCON (F07TGF) to estimate the reciprocal condition
! number of R
CALL dtrcon('Infinity-norm','Upper','Non-unit',irank,a(1,n-irank+1), &
lda,rcond,work,iwork,info)
WRITE (nout,*)
WRITE (nout,*) 'Estimate of reciprocal condition number for R'
WRITE (nout,99997) rcond
WRITE (nout,*)
! So long as irank = n, get the machine precision, eps, and
! compute the approximate error bound for the computed
! generalized singular values
IF (irank==n) THEN
eps = x02ajf()
serrbd = eps/rcond
WRITE (nout,*) &
'Error estimate for the generalized singular values'
WRITE (nout,99997) serrbd
ELSE
WRITE (nout,*) '(A**T B**T)**T is not of full rank'
END IF
ELSE
WRITE (nout,99996) 'Failure in DGGSVD. INFO =', info
END IF
99999 FORMAT (1X,I5)
99998 FORMAT (3X,8(1P,E12.4))
99997 FORMAT (1X,1P,E11.1)
99996 FORMAT (1X,A,I4)
END PROGRAM f08vafe