Keyword: 分散分析, ANOVA, 行と列配置, ラテン方格法
概要
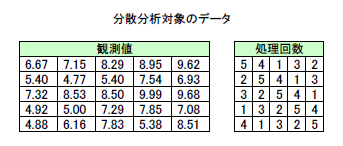
本サンプルは一般的な行と列配置の分散分析（ANOVA: Analysis of Variance) を行うFortranによるサンプルプログラムです。 本サンプルは以下に示される観測値をラテン方格法を用いて分散分析し、分散分析表、処理平均と処理平均の差の標準誤差を出力します。
※本サンプルはnAG Fortranライブラリに含まれるルーチン g04bcf() のExampleコードです。本サンプル及びルーチンの詳細情報は g04bcf のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
（本ルーチンの詳細はg04bcf のマニュアルページを参照）1 2 3 4 5 6 7 8 9 10 11 12
| このデータをダウンロード |
G04BCF Example Program Data 1 5 5 5 6.67 7.15 8.29 8.95 9.62 5.40 4.77 5.40 7.54 6.93 7.32 8.53 8.50 9.99 9.68 4.92 5.00 7.29 7.85 7.08 4.88 6.16 7.83 5.38 8.51 5 4 1 3 2 2 5 4 1 3 3 2 5 4 1 1 3 2 5 4 4 1 3 2 5
- １行目はタイトル行で読み飛ばされます。
- ２行目に反復数（nrep=1）、反復ごとの行数（nrow=5）、反復ごとの列数（ncol=5）と処理数（nt=5）を指定しています。
- ３～７行目に観測値のデータ(y)を指定しています。
- ８～１２行目に各観測値が何回目の処理で処理されるか処理回数(it)を指定しています。
出力結果
（本ルーチンの詳細はg04bcf のマニュアルページを参照）1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
| この出力例をダウンロード |
G04BCF Example Program Results
ANOVA TABLE
Rows 4. 29.4231 7.3558 9.0266 0.0013
Columns 4. 22.9950 5.7487 7.0545 0.0037
Treatments 4. 0.5423 0.1356 0.1664 0.9514
Residual 12. 9.7788 0.8149
Total 24. 62.7392
Treatment means
7.3180 7.2440 7.2060 6.9000 7.2600
S.E. of difference (orthogonal design) = 0.5709
- ３～９行目に分散分析表が出力されています。
- ５行目に行の自由度、平方和、平均平方、Ｆ統計量と有意水準が出力されています。
- ６行目に列の自由度、平方和、平均平方、Ｆ統計量と有意水準が出力されています。
- ７行目に処理の自由度、平方和、平均平方、Ｆ統計量と有意水準が出力されています。
- ８行目に残差の自由度、平方和、平均平方が出力されています。
- ９行目に自由度と平方和の合計が出力されています。
- １３行目には各処理の処理平均が出力されています。
- １５行目には処理平均の差の標準誤差が出力されています。
ソースコード
（本ルーチンの詳細はg04bcf のマニュアルページを参照）
※本サンプルソースコードは科学技術・統計計算ライブラリである「nAG Fortranライブラリ」のルーチンを呼び出します。
サンプルのコンパイル及び実行方法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81
| このソースコードをダウンロード |
PROGRAM g04bcfe
! G04BCF Example Program Text
! Mark 23 Release. nAG Copyright 2011.
! .. Use Statements ..
USE nag_library, ONLY : g04bcf, nag_wp
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Parameters ..
INTEGER, PARAMETER :: ldtabl = 6, nin = 5, nout = 6
! .. Local Scalars ..
REAL (KIND=nag_wp) :: gmean, tol
INTEGER :: ifail, irdf, ldc, lit, n, ncol, &
nrep, nrow, nt
! .. Local Arrays ..
REAL (KIND=nag_wp), ALLOCATABLE :: c(:,:), cmean(:), ef(:), r(:), &
rmean(:), rpmean(:), tmean(:), &
wk(:), y(:)
REAL (KIND=nag_wp) :: tabl(ldtabl,5)
INTEGER, ALLOCATABLE :: irep(:), it(:)
! .. Executable Statements ..
WRITE (nout,*) 'G04BCF Example Program Results'
WRITE (nout,*)
! Skip heading in data file
READ (nin,*)
! Read in the problem size
READ (nin,*) nrep, nrow, ncol, nt
n = nrep*nrow*ncol
IF (nt>1) THEN
lit = n
ELSE
lit = 1
END IF
ldc = nt
ALLOCATE (irep(nt),y(n),tmean(nt),it(lit),c(ldc,nt),rpmean(nrep), &
rmean(nrep*nrow),cmean(nrep*ncol),r(n),ef(nt),wk(3*nt))
! Read in the data
READ (nin,*) y(1:n)
IF (nt>1) THEN
READ (nin,*) it(1:n)
END IF
! Use default tolerance
tol = 0.0E0_nag_wp
! Use standard degrees of freedom
irdf = 0
! Calculate the ANOVA table
ifail = 0
CALL g04bcf(nrep,nrow,ncol,y,nt,it,gmean,tmean,tabl,ldtabl,c,ldc,irep, &
rpmean,rmean,cmean,r,ef,tol,irdf,wk,ifail)
! Display results
WRITE (nout,*) ' ANOVA TABLE'
WRITE (nout,*)
IF (nrep>1) THEN
WRITE (nout,99998) ' Reps ', tabl(1,1:5)
END IF
WRITE (nout,99998) ' Rows ', tabl(2,1:5)
WRITE (nout,99998) ' Columns ', tabl(3,1:5)
WRITE (nout,99998) ' Treatments ', tabl(4,1:5)
WRITE (nout,99998) ' Residual ', tabl(5,1:3)
WRITE (nout,99998) ' Total ', tabl(6,1:2)
WRITE (nout,*)
WRITE (nout,*) ' Treatment means'
WRITE (nout,*)
WRITE (nout,99999) tmean(1:nt)
WRITE (nout,*)
WRITE (nout,99997) ' S.E. of difference (orthogonal design) = ', c(2,1)
99999 FORMAT (10F10.4)
99998 FORMAT (A,F3.0,2X,3(F10.4,2X),F8.4)
99997 FORMAT (A,F10.4)
END PROGRAM g04bcfe