数学的問題の定式化

この短いセクションにおいては問題を的確にモデル化することの重要性について触れておきたい。ただしそれに対する深遠な解決策を提言するわけではない。

Well-conditionedな問題をill-conditionedな問題にしてしまうことはいともたやすくできる。例えばExample 4.10においてはwell-conditionedな数値積分の問題 MATH を前進漸化式 MATH によって $y_{n}$ を求めるというill-conditionedな問題に変換してしまった。

別の例をあげれば、セクション4.3において多項式は非常にill-conditionedなものとなり得ることを示した。それ故、行列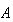の固有値の計算はほぼ間違いなくの特性方程式を介して計算されるべきではない。例えばが固有値 $\lambda_{i}=i,$ $i=1,2,\ldots,20$ を持つ対称行列であった場合、の特性方程式 $\det(A-\lambda A)$ は大変ill-conditionedなものとなる（Example 4.17参照）。

一方において対称行列の固有値は常にwell-conditionedである [Wilkinson, 1965, Section 31, Chapter 2]。

上記2つの例は数学的問題を変形する際の危険性を示している。Ill-conditionedな数学的な問題は物理的な問題のモデル化が貧弱であるがためにもたらされることが良くある。従ってモデル化プロセスの全体について注意を払う必要がある。

問題の定式化がまずかった場合には、満足の行かない解が得られたとしてもソフトウェアにその責めを負わせることはできない。ただしその場合でも、問題の条件(condition)に関する尺度、あるいは解の精度に関する何らかの尺度を提供するようにソフトウェアに対して期待することはできる。

不適切なスケーリングに伴う悪影響を回避する上で計測単位の選択にも注意を払うべきであることについては、セクション4.1の末尾で言及した。