条件、安定性、誤差解析
条件
まず問題の条件について見て行こう。ある問題の条件(condition)とはデータの摂動に対し問題がどう反応するかという感度(sensitivity)に関係したものである。データの小さな変動によって解が比較的大きく変化する場合には、問題はill-conditionedであると言う。そうでない場合はwell-conditionedであると言う。条件とは問題の感度に関する話であり、問題解法の手法とは無関係である点に注意する必要がある。ここではill-conditionedな問題の例をいくつか示すことにする。
Example 4.1
(3次方程式)
厳密解 を持つ3次方程式
を持つ3次方程式 について考える。今、
について考える。今、 の係数をわずかに変化させ、
の係数をわずかに変化させ、 とすると、その根は
とすると、その根は となる。従って2つの根
となる。従って2つの根 に対する変動は係数の変化よりもはるかに大きい。一方、3次方程式
に対する変動は係数の変化よりもはるかに大きい。一方、3次方程式 の解は
の解は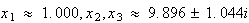 となり、重根は2つの共役複素数に分かれることになる(虚数部の値もそれなりに大きい)。
となり、重根は2つの共役複素数に分かれることになる(虚数部の値もそれなりに大きい)。
この場合、根 はill-conditionedである。ただしこのデータからだけだと、
はill-conditionedである。ただしこのデータからだけだと、 の条件について何かを演繹することはできない。図3はこれら3本の3次多項式をプロットしたものである。
の条件について何かを演繹することはできない。図3はこれら3本の3次多項式をプロットしたものである。

図3 3次方程式の例

Example 4.2
(固有値問題)
行列 は固有値
は固有値 を持つが、それにわずかな摂動を加えた行列
を持つが、それにわずかな摂動を加えた行列 の固有値は
の固有値は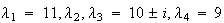 となる。
となる。
Example 4.3 (積分)

 であれば
であれば であるが、
であるが、 のときには
のときには となる。
となる。 の場合の関数
の場合の関数 の形状を図4に示す。ただし縦軸のスケールファクタが
の形状を図4に示す。ただし縦軸のスケールファクタが である点に注意。このため関数式のわずかな変化によって定積分の値(曲線下の面積)は大きく変化することになる。
である点に注意。このため関数式のわずかな変化によって定積分の値(曲線下の面積)は大きく変化することになる。

図4 積分の例

Example 4.4
(連立1次方程式)
 で与えられる連立1次方程式
で与えられる連立1次方程式
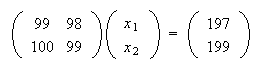
|
(5) |
 という解を有するが、
という解を有するが、

|
 となる。数式
(5)で表される2本の直線をプロットしたものが図5であるが、この解像度では2本を識別することはできない。
となる。数式
(5)で表される2本の直線をプロットしたものが図5であるが、この解像度では2本を識別することはできない。

図5 連立1次方程式の例

問題がill-conditionedであるか否かを決定できるようにするためには、その条件に関し何らかの尺度があることが望ましい。そのような尺度が得られる2つの簡単なケースを紹介すると共に、3番目の例については結果を引用する。第1のケースについては1変数関数の評価に関する条件数(condition
number)を導出する [Higham, 2002, Section
1.6]。
今、関数を とし、
とし、 は2回微分可能で
は2回微分可能で であるとする。また
であるとする。また とする。このとき平均値の定理より
とする。このとき平均値の定理より
これより
このとき は
は の条件数(condition
number)と呼ばれる。なぜなら
の条件数(condition
number)と呼ばれる。なぜなら だからである。従って
だからである。従って が大きな値の場合には問題はill-conditionedとなる。すなわち
が大きな値の場合には問題はill-conditionedとなる。すなわち のわずかな変動が解
のわずかな変動が解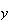 の大きな変動をもたらすことになる。
の大きな変動をもたらすことになる。
Example 4.5
 とする。このとき
とする。このとき となるため、
となるため、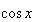 は
は の漸近線に近い部分、例えば
の漸近線に近い部分、例えば が
が (Note1)に近い部分で最も鋭敏に反応することがわかる。例えば
(Note1)に近い部分で最も鋭敏に反応することがわかる。例えば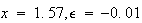 とすると
とすると となる。これは
となる。これは の非常に良い推定値であると言える。
の非常に良い推定値であると言える。
第2の例として連立1次方程式 の条件数について考えてみる。今、
の条件数について考えてみる。今、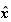 を摂動を加えた方程式
を摂動を加えた方程式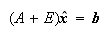 の解とするとき、
の解とするとき、
これより

|
(6) |
このとき を方程式
を方程式 の解に関する
の解に関する の条件数、あるいは逆行列操作(matrix
inversion)に関する
の条件数、あるいは逆行列操作(matrix
inversion)に関する の条件数と呼ぶ。
の条件数と呼ぶ。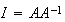 であるから、
であるから、 となるような任意のノルム(norm)に対して
となるような任意のノルム(norm)に対して が言える。ここに等号は
が言える。ここに等号は ノルムの場合に成り立つ。
ノルムの場合に成り立つ。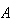 が特異(singular)である場合には
が特異(singular)である場合には となる。
となる。
Example 4.6
(行列の条件)
Example
4.4の行列の場合、 及び
及び より
より
従って の精度が4桁程度である場合には解の精度が全く期待できないことがわかる。
の精度が4桁程度である場合には解の精度が全く期待できないことがわかる。
条件数という用語は連立1次方程式との関連においてTuringによって初めて用いられた
[Turing,
1948]。直交、またはユニタリ行列 の場合には
の場合には となる点に注意。
となる点に注意。
第3の例としてここでは多項式の根の感度(sensitivity)に関する結果を引用することにする。今、多項式を とし、
とし、 を
を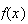 の単根であるとする。このとき
の単根であるとする。このとき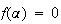 であるが、
であるが、 である。次に
である。次に を摂動を加えた多項式を
を摂動を加えた多項式を とし、その根を
とし、その根を とする(
とする( )。このとき
[Wilkinson, 1963, Section 7, Chapter 2]
によれば
)。このとき
[Wilkinson, 1963, Section 7, Chapter 2]
によれば であることが示される。Wilkinsonはさらに
であることが示される。Wilkinsonはさらに が重根である場合に
が重根である場合に という式を導いている。
という式を導いている。
Example 4.7
(3次方程式の根の条件)
Example
4.1の3次方程式の根 に対し、
に対し、 とすると
とすると より
より
従ってこの根は の係数値の摂動に対し大変well-conditionedであると言える。一方、重根
の係数値の摂動に対し大変well-conditionedであると言える。一方、重根 については
については より
より
従って の摂動によって根に対してはかなり大きな摂動が加わることがわかる。
の摂動によって根に対してはかなり大きな摂動が加わることがわかる。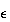 は特に小さいというわけではないので、
は特に小さいというわけではないので、 の推定値は特別に正確とは言えないが、ill-conditioningに関する警告としては十分である。
の推定値は特別に正確とは言えないが、ill-conditioningに関する警告としては十分である。
Higham [2002, Section 25.4]
には一般的な非線形方程式の根の感度に関する結果が示されている。
スケーリングが適切でない(しばしば計測単位の選択のまずさから起る)というだけで問題がill-conditionedとなることがある。アルゴリズム、あるいはその実装によってはスケーリングの影響を受けない、あるいは自動スケーリングを試みるものもあるが、そうでない場合には、スケーリングの選択が良い結果を得る上で重要な要因となることがある。スケーリングが不適切な問題は容易に本質的にill-conditionedな問題に変貌し得る。
Example 4.8
(スケーリングが不適切な行列)
行列 を
を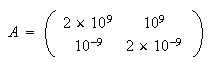 とするとき
とするとき となるため、
となるため、 はill-conditionedである。しかし
はill-conditionedである。しかし に対し次のようなスケーリングを施した場合、
に対し次のようなスケーリングを施した場合、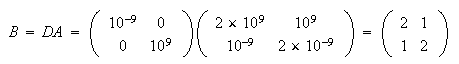
 に対しては
に対しては となるため、
となるため、 はwell-conditionedであると言える。一方
はwell-conditionedであると言える。一方 を使い、
を使い、 として平面の回転を行うと
として平面の回転を行うと となる。ここで
となる。ここで は直交行列であるため
は直交行列であるため 、従って
、従って は
は と同様ill-conditionedとなる。しかしこの場合にはスケーリングによって事態は改善されない。
と同様ill-conditionedとなる。しかしこの場合にはスケーリングによって事態は改善されない。 は近似的に
は近似的に と書けるが、これは特異行列である。従って
と書けるが、これは特異行列である。従って は本質的にill-conditionedである。倍精度のIEEE
arithmeticではこれが
は本質的にill-conditionedである。倍精度のIEEE
arithmeticではこれが の浮動小数表現となる。
の浮動小数表現となる。
LAPACKルーチンの多くがスケーリングを行ったり、連立1次方程式の場合には行列を平衡化(equilibrate)させたり [Anderson et al., 1999, Sections 2.4.1 and 4.4.1], [Higham, 2002, Sections 7.3 and 9.8]、固有値問題の場合にはバランスさせたり [Anderson et al., 1999, Sections 4.8.1.2 and 4.11.1.2] するオプションを用意している。
