数値解に関する問題点
このセクションでは合理的な解を得るためには注意を要する数値計算のいくつかの例について考察してみよう。なお、本セクション、及び後続のセクション中におけるほとんどの用例ではround
to
nearestの10進の浮動小数(有効数字(significant
figure))演算が用いられている。
最初の例は破壊的な減算(通常桁落ち(cancellation)と呼ばれる)の問題に関するものである。
Example 3.1
(桁落ち)
4桁の10進演算を用い、 の計算を行いたいものとする。標準的なやり方で左から右へ計算して行くと、正しい結果である
の計算を行いたいものとする。標準的なやり方で左から右へ計算して行くと、正しい結果である ではなく
ではなく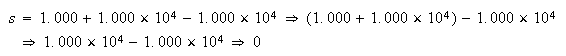 という結果が得られてしまう。減算は厳密に行われたわけであるが、解に関するすべての情報は失われてしまっている。
という結果が得られてしまう。減算は厳密に行われたわけであるが、解に関するすべての情報は失われてしまっている。
Example
3.1が示すように、みじめな結果の原因は桁落ち以前にあり、桁落ち自体は棺に対する最後の釘でしかないことがしばしば起る。Example
3.1の場合、損傷は の計算中に起きている。すなわち重要な情報(
の計算中に起きている。すなわち重要な情報( )がこの過程で失われている。ほとんど等しい値同士の減算が常に破壊的であるというわけではない。
)がこの過程で失われている。ほとんど等しい値同士の減算が常に破壊的であるというわけではない。
多くの問題においては、理論的には等価であっても相異なる定式化(alternative
formulations)がいくつか存在し、数値計算上全く異なる結果がもたらされることが起り得る。次に示すのは標本分散の計算における例である。
Example 3.2
(標本分散 Note1 )
 個の値
個の値 からなる集合の標本分散は
からなる集合の標本分散は

|
(2) |
 は
は 個の値の標本平均
個の値の標本平均
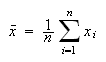
|

|
(3) |
今、 とし、8桁の演算を行うとすると、
(2)
は正しい値である
とし、8桁の演算を行うとすると、
(2)
は正しい値である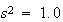 という結果をもたらすが、
(3)
は
という結果をもたらすが、
(3)
は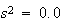 という相対誤差が
という相対誤差が の結果をもたらす。
の結果をもたらす。
(3)では明らかに桁落ちの問題が発生している。一方
(2)
は が非常に大きな値でない限り常に良好な結果をもたらす
[Higham, 2002, Problem
1.10]。標本分散の計算に絡む問題点については
Chan etal. [1983]
も参照されたい。
が非常に大きな値でない限り常に良好な結果をもたらす
[Higham, 2002, Problem
1.10]。標本分散の計算に絡む問題点については
Chan etal. [1983]
も参照されたい。
ソフトウェアパッケージや電卓がアルゴリズム
(3)
を実装していることは残念ながら既定の事実である。例えばMicrosoft
Office XPのExcel
2002(及びそれ以前のExcelも同様)において、関数STDEVを使ってデータ の標準偏差を計算させると、
の標準偏差を計算させると、 という結果が得られる。Excelが広範囲で使用されていること、及び標準偏差とそのアプリケーション中での重要度を考え合わせるなら、Excelのこれらのバージョンにおいて
(3)
が用いられてきたということは失望させられる事実である。 (Note2) さらなる情報については
Cox et al. [2000], Knüsel [1998], McCullough and Wilson [1999],
McCullough and Wilson [2002]
を参照。OpenOffice.orgバージョン1.0.2のスプレッドシートも同じ結果を出力するが、ヘルプシステムを見てもどの手法が用いられているかについてはわからない。一方、Gnumericのスプレッドシート(バージョン1.0.12)はその手法まではわからないものの、正しい結果を出力する。
という結果が得られる。Excelが広範囲で使用されていること、及び標準偏差とそのアプリケーション中での重要度を考え合わせるなら、Excelのこれらのバージョンにおいて
(3)
が用いられてきたということは失望させられる事実である。 (Note2) さらなる情報については
Cox et al. [2000], Knüsel [1998], McCullough and Wilson [1999],
McCullough and Wilson [2002]
を参照。OpenOffice.orgバージョン1.0.2のスプレッドシートも同じ結果を出力するが、ヘルプシステムを見てもどの手法が用いられているかについてはわからない。一方、Gnumericのスプレッドシート(バージョン1.0.12)はその手法まではわからないものの、正しい結果を出力する。
演算結果が浮動小数として表現できる最大の数を超えた場合はオーバフロー(overflow)と呼ばれる。例えば倍精度のIEEE
arithmeticの場合、その値の範囲は概ね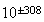 であるため、
であるため、 とすると
とすると はオーバフローをもたらす。同様に
はオーバフローをもたらす。同様に はアンダフロー(underflow)と呼ばれる。なぜなら表現可能な最小の浮動小数(非負)よりも小さな値となってしまうからである。
はアンダフロー(underflow)と呼ばれる。なぜなら表現可能な最小の浮動小数(非負)よりも小さな値となってしまうからである。
セクションieee
arithmeticにおいて議論した単位丸め誤差(unit
rounding
error)やマシン の場合と同様、オーバフローやアンダフローに対する閾値も、LAPACK関数S/DLAMCHを用いて(引数CMACHをそれぞれ
の場合と同様、オーバフローやアンダフローに対する閾値も、LAPACK関数S/DLAMCHを用いて(引数CMACHをそれぞれ'o',
'u'と指定する)、nAG
Fortran
Libraryに対してはそれぞれルーチンX02ALFとX02AKFを用いて、Matlabに対しては組込み変数realmax,
realminを用いて、Fortran
95に対しては数値問合せ関数huge,
tinyを用いて、求めることができる。
不必要なオーバフローや破壊的なアンダフローを回避するには注意が必要である。次は図2に示されるような直角三角形の斜辺の長さを計算する際に、どのような注意を払う必要があるかを示す例である。

図2 直角三角形の斜辺
Example 3.3 (斜辺)
図2において または
または が非常に大きな値の場合、たとえ
が非常に大きな値の場合、たとえ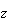 が表現可能であったとしてもオーバフローの危険性がある。
が表現可能であったとしてもオーバフローの危険性がある。 が負ではないとき、
が負ではないとき、 を計算する安全な方法は次のとおりである。
を計算する安全な方法は次のとおりである。

この計算法であれば、 双方がアンダフローしたとしても
双方がアンダフローしたとしても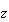 が
が となってしまうことを回避することができる。なお、Stewart
[1998, p.139, p.144]
は
となってしまうことを回避することができる。なお、Stewart
[1998, p.139, p.144]
は を
を のように計算すべきと推奨している。なぜならこの方が若干ではあるが16進法のマシン上でより正確なものとなるからである。ピタゴラスの平方和を計算するその他の興味深い手法については
Moler and Morrison [1983]
を参照されたい。また
Dubrulle [1983] や Higham and Higham [2005, section 22.9]
も参考になる。
のように計算すべきと推奨している。なぜならこの方が若干ではあるが16進法のマシン上でより正確なものとなるからである。ピタゴラスの平方和を計算するその他の興味深い手法については
Moler and Morrison [1983]
を参照されたい。また
Dubrulle [1983] や Higham and Higham [2005, section 22.9]
も参考になる。
Example
3.2の(3)もまたオーバフロー、アンダフローの可能性を秘めている。実際、Excelはより安定なものではなくこの数式を実装すると同時に、アンダフロー、オーバフローを回避する措置も講じていないことがわかる。例えば E
E E
E という値に対し、Microsoft
Office 2003のExcel
2003に含まれるSTDEVは不可解な
という値に対し、Microsoft
Office 2003のExcel
2003に含まれるSTDEVは不可解な#NUM!という記号を応答として返してくる。これは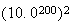 がIEEE倍精度演算においてオーバフローを起したことによる数値例外を示すものである。正しい標準偏差の値はもちろん
がIEEE倍精度演算においてオーバフローを起したことによる数値例外を示すものである。正しい標準偏差の値はもちろん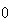 である。同様に
である。同様に E
E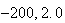 E
E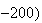 という値に対し、STDEVは正しい値
という値に対し、STDEVは正しい値 E
E ではなく
ではなく という値を返してくる。OpenOffice.orgバージョン1.0.2もまたこのデータに対しては
という値を返してくる。OpenOffice.orgバージョン1.0.2もまたこのデータに対しては を応答し、先のデータに対してはオーバフローを生ずる。Excelを模倣するのも常に良い結果を生むとは限らない。
を応答し、先のデータに対してはオーバフローを生ずる。Excelを模倣するのも常に良い結果を生むとは限らない。
複素数 の絶対値(modulus)の計算でもExample
3.3の場合とほぼ同様の計算が必要となる。
の絶対値(modulus)の計算でもExample
3.3の場合とほぼ同様の計算が必要となる。
Example 3.4
(複素数の絶対値)



この計算法であれば、 双方がアンダフローしたとしても
双方がアンダフローしたとしても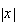 が
が となってしまうことを回避することができる。
となってしまうことを回避することができる。
複素数の計算において注意が必要となる別のケースは除算である。
この場合もオーバフロー、アンダフローを回避するためには何らかのスケーリングが必要となる。具体例については
Smith [1962], Stewart [1985], Priest [2004]
を参照されたい。Algol
60における複素数の絶対値、除算、平方根の算出方法については
Martin and Wilkinson [1968]
を参照。複素数演算用のnAG
Library Chapter,
A02にはこれらAlgolのプロシジャをベースにしたルーチンが含まれているが、その用例については
nAG [2003]
を参照。また注意深く設計されたC関数については上記
Priest [2004]
に記述が見られる。複素数の浮動小数演算のある側面については誤って実装されている場合もあるが、その具体例については
Blackford et al. [1997, Section 7]
を参照されたい。
オーバフローと破壊的なアンダフローの回避に関する注意が要求される別の例は実平面の回転に伴う計算である。この場合、 としたとき、
としたとき、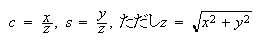 あるいは
あるいは の計算が必要となる。別の書き方をするなら
の計算が必要となる。別の書き方をするなら

|
(4) |
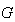 とすると
とすると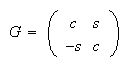 従って(4)
より
従って(4)
より となる。
となる。
ゼロの導出のためにこのように用いられたとき、回転は一般的にGivens平面回転(Givens
plane rotation) [Givens, 1954; Golub and Van Loan, 1996]
と呼ばれる。Givens自身は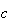 と
と の計算において確かに注意を払った。浮動小数の値域を通して可能な限り精度を維持し、オーバフローと破壊的なアンダフローを回避できる一見簡単そうなアルゴリズム(しかし効率の良いもの)を実装する際に必要となる詳細な注意事項については
Bindel et al. [2002]
を参照。Givens平面回転に関する計算法の詳細が記述されている。
の計算において確かに注意を払った。浮動小数の値域を通して可能な限り精度を維持し、オーバフローと破壊的なアンダフローを回避できる一見簡単そうなアルゴリズム(しかし効率の良いもの)を実装する際に必要となる詳細な注意事項については
Bindel et al. [2002]
を参照。Givens平面回転に関する計算法の詳細が記述されている。
計算結果はある意味では妥当と言えても、ユーザが期待していたものとは異なるといったことが時折起る。次の例の場合、計算結果は厳密解に近いものであるが、ユーザが期待していた制約条件は満たしていない。
Example 3.5
(標本平均 Note_3 )
3桁の浮動小数10進演算を使用した場合、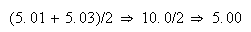 となり、計算結果は不正確というわけではないが、実際のデータ値の範囲からはずれた値となってしまう。
となり、計算結果は不正確というわけではないが、実際のデータ値の範囲からはずれた値となってしまう。
このような結果が問題となるかどうかはアプリケーションに依存するが、数値計算アルゴリズムを実装する際には考慮されなくてはならない問題である。例えば であるとき、
であるとき、 という性質が計算結果においても受け継がれ、
という性質が計算結果においても受け継がれ、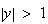 となるような結果が返されることはあり得ないものと我々は期待する。単調関数について言えば、その単調性(monotonicity)は計算結果においても温存されるものと期待することになる。
となるような結果が返されることはあり得ないものと我々は期待する。単調関数について言えば、その単調性(monotonicity)は計算結果においても温存されるものと期待することになる。
