製品 & サービス 
サポート 
ダウンロード 
リソース 
ご購入 
会社案内 
お問い合わせ 

複素一般化特異値分解: 複素行列ペアの一般化特異値分解

LAPACKサンプルソースコード : 使用ルーチン名：ZGGSVD

ホーム > LAPACKサンプルプログラム目次 > 複素一般化特異値分解 > 複素行列ペアの一般化特異値分解

概要

本サンプルはFortran言語によりLAPACKルーチンZGGSVDを利用するサンプルプログラムです。

一般化特異値分解を行います。

\begin{displaymath} A = U \Sigma_1 \left( \begin{array}{cc} 0 & R \end{array... ...a_2 \left( \begin{array}{cc} 0 & R \end{array} \right) Q^H, \end{displaymath}

ここで

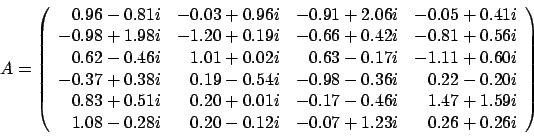
\begin{displaymath} A = \left( \begin{array}{rrrr} 0.96 - 0.81 i & -0.03 + 0.... ...- 0.12 i & -0.07 + 1.23 i & 0.26 + 0.26 i \end{array} \right) \end{displaymath}

及び

\begin{displaymath} B = \left( \begin{array}{rrrr} 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1 \end{array} \right), \end{displaymath}

$ R$の条件数の推定値と計算された一般化特異値の誤差限界も合わせて求めます。

この例題プログラムは $ m \ge n$であることを想定していますが、そうでない場合には若干のコード変更が必要です。

入力データ

（本ルーチンの詳細はZGGSVD のマニュアルページを参照） 
1
2
3
4
5
6
7
8
9
10
11
12
13
このデータをダウンロード 
ZGGSVD Example Program Data

  6             4             2                         :Values of M, N and P

( 0.96,-0.81) (-0.03, 0.96) (-0.91, 2.06) (-0.05, 0.41)
(-0.98, 1.98) (-1.20, 0.19) (-0.66, 0.42) (-0.81, 0.56)
( 0.62,-0.46) ( 1.01, 0.02) ( 0.63,-0.17) (-1.11, 0.60)
( 0.37, 0.38) ( 0.19,-0.54) (-0.98,-0.36) ( 0.22,-0.20)
( 0.83, 0.51) ( 0.20, 0.01) (-0.17,-0.46) ( 1.47, 1.59)
( 1.08,-0.28) ( 0.20,-0.12) (-0.07, 1.23) ( 0.26, 0.26) :End of matrix A

( 1.00, 0.00) ( 0.00, 0.00) (-1.00, 0.00) ( 0.00, 0.00)
( 0.00, 0.00) ( 1.00, 0.00) ( 0.00, 0.00) (-1.00, 0.00) :End of matrix B

出力結果

（本ルーチンの詳細はZGGSVD のマニュアルページを参照） 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
この出力例をダウンロード 
 ZGGSVD Example Program Results

 Number of infinite generalized singular values (K)
     2
 Number of finite generalized singular values (L)
     2
 Numerical rank of (A**H B**H)**H (K+L)
     4

 Finite generalized singular values
       2.0720E+00   1.1058E+00

 Unitary matrix U
                              1                           2
 1  ( -1.3038E-02, -3.2595E-01) ( -1.4039E-01, -2.6167E-01)
 2  (  4.2764E-01, -6.2582E-01) (  8.6298E-02, -3.8174E-02)
 3  ( -3.2595E-01,  1.6428E-01) (  3.8163E-01, -1.8219E-01)
 4  (  1.5906E-01, -5.2151E-03) ( -2.8207E-01,  1.9732E-01)
 5  ( -1.7210E-01, -1.3038E-02) ( -5.0942E-01, -5.0319E-01)
 6  ( -2.6336E-01, -2.4772E-01) ( -1.0861E-01,  2.8474E-01)
 
                              3                           4
 1  (  2.5177E-01, -7.9789E-01) ( -5.0956E-02, -2.1750E-01)
 2  ( -3.2188E-01,  1.6112E-01) (  1.1979E-01,  1.6319E-01)
 3  (  1.3231E-01, -1.4565E-02) ( -5.0671E-01,  1.8615E-01)
 4  (  2.1598E-01,  1.8813E-01) ( -4.0163E-01,  2.6787E-01)
 5  (  3.6488E-02,  2.0316E-01) (  1.9271E-01,  1.5574E-01)
 6  (  1.0906E-01, -1.2712E-01) ( -8.8159E-02,  5.6169E-01)
 
                              5                           6
 1  ( -4.5947E-02,  1.4052E-04) ( -5.2773E-02, -2.2492E-01)
 2  ( -8.0311E-02, -4.3605E-01) ( -3.8117E-02, -2.1907E-01)
 3  (  5.9714E-02, -5.8974E-01) ( -1.3850E-01, -9.0941E-02)
 4  ( -4.6443E-02,  3.0864E-01) ( -3.7354E-01, -5.5148E-01)
 5  (  5.7843E-01, -1.2439E-01) ( -1.8815E-02, -5.5686E-02)
 6  (  1.5763E-02,  4.7130E-02) (  6.5007E-01,  4.9173E-03)

 Unitary matrix V
                              1                           2
 1  (  9.8930E-01,  1.9041E-19) ( -1.1461E-01,  9.0250E-02)
 2  ( -1.1461E-01, -9.0250E-02) ( -9.8930E-01,  1.9041E-19)

 Unitary matrix Q
                              1                           2
 1  (  7.0711E-01,  0.0000E+00) (  0.0000E+00,  0.0000E+00)
 2  (  0.0000E+00,  0.0000E+00) (  7.0711E-01,  0.0000E+00)
 3  (  7.0711E-01,  0.0000E+00) (  0.0000E+00,  0.0000E+00)
 4  (  0.0000E+00,  0.0000E+00) (  7.0711E-01,  0.0000E+00)
 
                              3                           4
 1  (  6.9954E-01,  4.7274E-19) (  8.1044E-02, -6.3817E-02)
 2  ( -8.1044E-02, -6.3817E-02) (  6.9954E-01, -4.7274E-19)
 3  ( -6.9954E-01, -4.7274E-19) ( -8.1044E-02,  6.3817E-02)
 4  (  8.1044E-02,  6.3817E-02) ( -6.9954E-01,  4.7274E-19)

 Nonsingular upper triangular matrix R
                              1                           2
 1  ( -2.7118E+00,  0.0000E+00) ( -1.4390E+00, -1.0315E+00)
 2                              ( -1.8583E+00,  0.0000E+00)
 3
 4
 
                              3                           4
 1  ( -7.6930E-02,  1.3613E+00) ( -2.8137E-01, -3.2425E-02)
 2  ( -1.0760E+00,  3.1016E-02) (  1.3292E+00,  3.6772E-01)
 3  (  3.2537E+00,  0.0000E+00) ( -6.3858E-17,  6.3858E-17)
 4                              ( -2.1084E+00,  0.0000E+00)

 Estimate of reciprocal condition number for R
       1.3E-01

 Error estimate for the generalized singular values
       1.7E-15

ソースコード

（本ルーチンの詳細はZGGSVD のマニュアルページを参照）

※本サンプルソースコードのご利用手順は「サンプルのコンパイル及び実行方法」をご参照下さい。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
このソースコードをダウンロード 
    Program zggsvd_example

!     ZGGSVD Example Program Text

!     Copyright 2017, Numerical Algorithms Group Ltd. http://www.nag.com

!     .. Use Statements ..
      Use lapack_example_aux, Only: nagf_file_print_matrix_complex_gen_comp
      Use lapack_interfaces, Only: zggsvd3, ztrcon
      Use lapack_precision, Only: dp
!     .. Implicit None Statement ..
      Implicit None
!     .. Parameters ..
      Integer, Parameter :: nin = 5, nout = 6
!     .. Local Scalars ..
      Real (Kind=dp) :: eps, rcond, serrbd
      Integer :: i, ifail, info, irank, j, k, l, lda, ldb, ldq, ldu, ldv, &
        lwork, m, n, p
!     .. Local Arrays ..
      Complex (Kind=dp), Allocatable :: a(:, :), b(:, :), q(:, :), u(:, :), &
        v(:, :), work(:)
      Real (Kind=dp), Allocatable :: alpha(:), beta(:), rwork(:)
      Integer, Allocatable :: iwork(:)
      Character (1) :: clabs(1), rlabs(1)
!     .. Intrinsic Procedures ..
      Intrinsic :: epsilon
!     .. Executable Statements ..
      Write (nout, *) 'ZGGSVD Example Program Results'
      Write (nout, *)
      Flush (nout)
!     Skip heading in data file
      Read (nin, *)
      Read (nin, *) m, n, p
      lda = m
      ldb = p
      ldq = n
      ldu = m
      ldv = p
      Allocate (a(lda,n), b(ldb,n), q(ldq,n), u(ldu,m), v(ldv,p), work(m+3*n), &
        alpha(n), beta(n), rwork(2*n), iwork(n))

!     Read the m by n matrix A and p by n matrix B from data file

      Read (nin, *)(a(i,1:n), i=1, m)
      Read (nin, *)(b(i,1:n), i=1, p)

!     Compute the generalized singular value decomposition of (A, B)
!     (A = U*D1*(0 R)*(Q**H), B = V*D2*(0 R)*(Q**H), m.ge.n)
      lwork = m + 3*n
      Call zggsvd3('U', 'V', 'Q', m, n, p, k, l, a, lda, b, ldb, alpha, beta, &
        u, ldu, v, ldv, q, ldq, work, lwork, rwork, iwork, info)

      If (info==0) Then

!       Print solution

        irank = k + l
        Write (nout, *) 'Number of infinite generalized singular values (K)'
        Write (nout, 100) k
        Write (nout, *) 'Number of finite generalized singular values (L)'
        Write (nout, 100) l
        Write (nout, *) 'Numerical rank of (A**H B**H)**H (K+L)'
        Write (nout, 100) irank
        Write (nout, *)
        Write (nout, *) 'Finite generalized singular values'
        Write (nout, 110)(alpha(j)/beta(j), j=k+1, irank)

        Write (nout, *)
        Flush (nout)

!       ifail: behaviour on error exit
!              =0 for hard exit, =1 for quiet-soft, =-1 for noisy-soft
        ifail = 0
        Call nagf_file_print_matrix_complex_gen_comp('General', ' ', m, m, u, &
          ldu, 'Bracketed', '1P,E12.4', 'Unitary matrix U', 'Integer', rlabs, &
          'Integer', clabs, 80, 0, ifail)

        Write (nout, *)
        Flush (nout)

        Call nagf_file_print_matrix_complex_gen_comp('General', ' ', p, p, v, &
          ldv, 'Bracketed', '1P,E12.4', 'Unitary matrix V', 'Integer', rlabs, &
          'Integer', clabs, 80, 0, ifail)

        Write (nout, *)
        Flush (nout)

        Call nagf_file_print_matrix_complex_gen_comp('General', ' ', n, n, q, &
          ldq, 'Bracketed', '1P,E12.4', 'Unitary matrix Q', 'Integer', rlabs, &
          'Integer', clabs, 80, 0, ifail)

        Write (nout, *)
        Flush (nout)

        Call nagf_file_print_matrix_complex_gen_comp('Upper triangular', &
          'Non-unit', irank, irank, a(1,n-irank+1), lda, 'Bracketed', &
          '1P,E12.4', 'Nonsingular upper triangular matrix R', 'Integer', &
          rlabs, 'Integer', clabs, 80, 0, ifail)

!       Call ZTRCON to estimate the reciprocal condition
!       number of R

        Call ztrcon('Infinity-norm', 'Upper', 'Non-unit', irank, &
          a(1,n-irank+1), lda, rcond, work, rwork, info)

        Write (nout, *)
        Write (nout, *) 'Estimate of reciprocal condition number for R'
        Write (nout, 120) rcond
        Write (nout, *)

!       So long as irank = n, get the machine precision, eps, and
!       compute the approximate error bound for the computed
!       generalized singular values

        If (irank==n) Then
          eps = epsilon(1.0E0_dp)
          serrbd = eps/rcond
          Write (nout, *) 'Error estimate for the generalized singular values'
          Write (nout, 120) serrbd
        Else
          Write (nout, *) '(A**H B**H)**H is not of full rank'
        End If
      Else
        Write (nout, 130) 'Failure in ZGGSVD3. INFO =', info
      End If

100   Format (1X, I5)
110   Format (4X, 8(1P,E13.4))
120   Format (3X, 1P, E11.1)
130   Format (1X, A, I4)
    End Program


ご案内
関連情報
© 日本ニューメリカルアルゴリズムズグループ株式会社 2025
Privacy Policy  /  Trademarks