ZGELS(複素線形最小二乗) LAPACKサンプルソースコード

ホーム > LAPACKサンプルプログラム目次 > 複素線形最小二乗 > QR 分解もしく LQ 分解

概要

本サンプルはFortran言語によりLAPACKルーチンZGELSを利用するサンプルプログラムです。

以下の線形最小二乗問題を解きます。

$\begin{displaymath}\min_{x} \left\Vert b - A x \right\Vert _{2}\end{displaymath}$

ここで

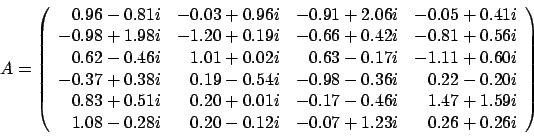
$\begin{displaymath}A = \left(\begin{array}{rrrr}0.96 - 0.81 i & -0.03 + 0.......- 0.12 i & -0.07 + 1.23 i & 0.26 + 0.26 i\end{array} \right)\end{displaymath}$

及び

$\begin{displaymath}b = \left(\begin{array}{r}-2.09 + 1.93 i \\3.34 - 3.......i \\-5.19 + 3.63 i \\0.98 + 2.53 i\end{array} \right).\end{displaymath}$

入力データ（本ルーチンの詳細は ZGELS のマニュアルページを参照）

このデータをダウンロード

ZGELS Example Program Data

   6             4                               :Values of M, N and NRHS

 ( 0.96,-0.81) (-0.03, 0.96) (-0.91, 2.06) (-0.05, 0.41)
 (-0.98, 1.98) (-1.20, 0.19) (-0.66, 0.42) (-0.81, 0.56)
 ( 0.62,-0.46) ( 1.01, 0.02) ( 0.63,-0.17) (-1.11, 0.60)
 (-0.37, 0.38) ( 0.19,-0.54) (-0.98,-0.36) ( 0.22,-0.20)
 ( 0.83, 0.51) ( 0.20, 0.01) (-0.17,-0.46) ( 1.47, 1.59)
 ( 1.08,-0.28) ( 0.20,-0.12) (-0.07, 1.23) ( 0.26, 0.26) :End of matrix A

 (-2.09, 1.93)
 ( 3.34,-3.53)
 (-4.94,-2.04)
 ( 0.17, 4.23)
 (-5.19, 3.63)
 ( 0.98, 2.53)                                           :End of vector b

出力結果

（本ルーチンの詳細はZGELS のマニュアルページを参照）

この出力例をダウンロード

 ZGELS Example Program Results

 Least squares solution
 (-0.5044,-1.2179) (-2.4281, 2.8574) ( 1.4872,-2.1955) ( 0.4537, 2.6904)

 Square root of the residual sum of squares
   6.88E-02

ソースコード

（本ルーチンの詳細はZGELS のマニュアルページを参照）

※本サンプルソースコードのご利用手順は「サンプルのコンパイル及び実行方法」をご参照下さい。

このソースコードをダウンロード

    Program zgels_example

!     ZGELS Example Program Text

!     Copyright 2017, Numerical Algorithms Group Ltd. http://www.nag.com

!     .. Use Statements ..
      Use blas_interfaces, Only: dznrm2
      Use lapack_interfaces, Only: zgels
      Use lapack_precision, Only: dp
!     .. Implicit None Statement ..
      Implicit None
!     .. Parameters ..
      Integer, Parameter :: nb = 64, nin = 5, nout = 6
!     .. Local Scalars ..
      Real (Kind=dp) :: rnorm
      Integer :: i, info, lda, lwork, m, n
!     .. Local Arrays ..
      Complex (Kind=dp), Allocatable :: a(:, :), b(:), work(:)
!     .. Executable Statements ..
      Write (nout, *) 'ZGELS Example Program Results'
      Write (nout, *)
!     Skip heading in data file
      Read (nin, *)
      Read (nin, *) m, n
      lda = m
      lwork = n + nb*m
      Allocate (a(lda,n), b(m), work(lwork))

!     Read A and B from data file

      Read (nin, *)(a(i,1:n), i=1, m)
      Read (nin, *) b(1:m)

!     Solve the least squares problem min( norm2(b - Ax) ) for x
      Call zgels('No transpose', m, n, 1, a, lda, b, m, work, lwork, info)

!     Print solution

      Write (nout, *) 'Least squares solution'
      Write (nout, 100) b(1:n)

!     Compute and print estimate of the square root of the residual
!     sum of squares

      rnorm = dznrm2(m-n, b(n+1), 1)
      Write (nout, *)
      Write (nout, *) 'Square root of the residual sum of squares'
      Write (nout, 110) rnorm

100   Format (4(' (',F7.4,',',F7.4,')',:))
110   Format (1X, 1P, E10.2)
    End Program

ご案内

複素線形最小二乗: QR 分解もしく LQ 分解

LAPACKサンプルソースコード : 使用ルーチン名：ZGELS

概要

出力結果

ソースコード